题目内容
1. 一半径为R的四分之三圆管竖直放置,圆心O与管口A的连线与地面齐平.一质量为m,半径略小于圆管内径的小球从离A管口H=2R高处正对管口由静止释放,后经B管口飞出,不计空气阻力,小球直径可忽略不计,以下说法正确的是( )
一半径为R的四分之三圆管竖直放置,圆心O与管口A的连线与地面齐平.一质量为m,半径略小于圆管内径的小球从离A管口H=2R高处正对管口由静止释放,后经B管口飞出,不计空气阻力,小球直径可忽略不计,以下说法正确的是( )| A. | 若圆管内壁光滑,小球落地点与O点距离为2R | |
| B. | 若小球落地点与O点距离为1.5R,经过B管口时对管口压力为$\frac{9}{8}$mg | |
| C. | 若小球从B口飞出以后刚好落至A口,则此过程中小球损失的机械能$\frac{3}{4}$mgR | |
| D. | 若小球从B口飞出以后刚好落至A口,则小球与管壁间的弹力先变大后变小 |
分析 A、根据机械能守恒定律求出最高点的速度,再由平抛运动的规律即可求解小球的落点与O点间的距离;
B、由平抛运动的规律求出B点速度,再根据向心力公式即可求解经过B管口时对管口的压力;
C、根据平抛规律求出小球到达最高点的速度,减少的重力势能和增加的动能的差即为损失的机械能;
D、根据动能定理求出最低点速度,由向心力公式求出最低点的弹力和最高点的弹力,即可判断该选项.
解答 解:A、根据机械能守恒定律,有:$mgH=mgR+\frac{1}{2}m{v}_{\;}^{2}$,即:$mg•2R=mgR+\frac{1}{2}m{v}_{\;}^{2}$,解得:$v=\sqrt{2gR}$
离开B点做平抛运动有:$R=\frac{1}{2}g{t}_{\;}^{2}$,得:$t=\sqrt{\frac{2R}{g}}$
水平距离为:x=vt=$\sqrt{2gR}$$•\sqrt{\frac{2R}{g}}$=2R,故A正确;
B、根据平抛运动的规律得:$R=\frac{1}{2}g{t}_{\;}^{2}$,解得:$t=\sqrt{\frac{2R}{g}}$,x=vt,得:$v=\frac{x}{t}=\frac{1.5R}{t}$=$\frac{3R}{2}\sqrt{\frac{g}{2R}}$,根据牛顿第二定律得:${F}_{N}^{\;}+mg=m\frac{{v}_{\;}^{2}}{R}$,解得:${F}_{N}^{\;}$=$\frac{1}{8}$mg,故B错误;
C、小球从B刚好落至A口,根据平抛运动的规律,有:$R=\frac{1}{2}g{t}_{\;}^{2}$,解得:$t=\sqrt{\frac{2R}{g}}$,R=vt,得:$v=\frac{R}{t}=R\sqrt{\frac{g}{2R}}=\sqrt{\frac{gR}{2}}$,小球损失的机械能为:△E=$mg(2R-R)-\frac{1}{2}m(\sqrt{\frac{gR}{2}})_{\;}^{2}$=$\frac{3}{4}mgR$,故C正确;
D、根据动能定理有:$mg(H+R)=\frac{1}{2}m{v}_{\;}^{2}$,得小球到达最低点的速度为:$v=\sqrt{6gR}$,由向心力公式${F}_{N}^{\;}-mg=m\frac{{v}_{\;}^{2}}{R}$得:${F}_{N}^{\;}=7mg$;小球在最高点时,有:$mg-{F}_{N}^{′}=m\frac{{v}_{\;}^{2}}{R}$,解得:${F}_{N}^{′}=\frac{1}{2}mg$,可知小球与管壁间的弹力先变大后变小,故D正确;
故选:ACD
点评 本题关键明确小球的运动规律,结合牛顿第二定律、向心力公式、平抛运动的分运动公式和机械能守恒定律列式求解,不难.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案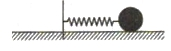 如图所示,原长为L,劲度系数为k的轻质弹簧拉着一个质量为m的小球在光滑的水平面上做匀速圆周运动.已知弹簧一直处于弹性限度内,则当弹簧的伸长量分别为L和2L时,下列说法正确的是( )
如图所示,原长为L,劲度系数为k的轻质弹簧拉着一个质量为m的小球在光滑的水平面上做匀速圆周运动.已知弹簧一直处于弹性限度内,则当弹簧的伸长量分别为L和2L时,下列说法正确的是( )| A. | 小球转动的角速度之比ω1:ω2=2:1 | |
| B. | 小球转动的线速度之比v1:v2=1:$\sqrt{3}$ | |
| C. | 小球的向心加速度之比为a1:a2=1:2 | |
| D. | 小球的周期之比为T1:T2=3:$\sqrt{3}$ |
 某物体在变力F作用下沿水平方向做直线运动,物体的质量m=10kg,F随物体的坐标x的变化关系如图所示.若物体从坐标原点处静止出发,不计一切摩擦,根据图示的F-x图象可求出物体运动到x=16m处时的速度大小为( )
某物体在变力F作用下沿水平方向做直线运动,物体的质量m=10kg,F随物体的坐标x的变化关系如图所示.若物体从坐标原点处静止出发,不计一切摩擦,根据图示的F-x图象可求出物体运动到x=16m处时的速度大小为( )| A. | 3m/s | B. | 4m/s | C. | 2$\sqrt{2}$m/s | D. | $\sqrt{17}$m/s |
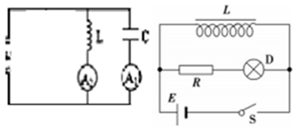 如甲图所示,交流电流表A1、A2分别与电容器C和电感线圈L串联后 接在同一个正弦式交流电源上,保持供电电压的最大值不变.如图乙图所示,电阻R和自感线圈L的电阻值都小于灯泡D的电阻,接通S,使电路达到稳定,灯泡D发光,下列说法正确的是( )
如甲图所示,交流电流表A1、A2分别与电容器C和电感线圈L串联后 接在同一个正弦式交流电源上,保持供电电压的最大值不变.如图乙图所示,电阻R和自感线圈L的电阻值都小于灯泡D的电阻,接通S,使电路达到稳定,灯泡D发光,下列说法正确的是( )| A. | 在图甲中,当供电电压的频率减少时,A1示数增大,A2示数减小 | |
| B. | 在图甲中,当供电电压的频率减小时,A1示数减小,A2示数增大 | |
| C. | 在图乙中,断开S后,D将渐渐变暗至熄灭 | |
| D. | 在图乙中,断开S后,D将变得更亮,然后渐渐变暗至熄灭 |
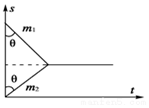 质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法不正确的是( )
质量分别为m1和m2的两个物体碰撞前后的位移-时间图象如图所示,以下说法不正确的是( )| A. | 碰撞前两物体动量相同 | |
| B. | 质量m1等于质量m2 | |
| C. | 碰撞后两物体一起做匀速直线运动 | |
| D. | 碰撞前两物体动量大小相等、方向相反 |
 如图所示,一小球自倾角θ=37°的斜面顶端A以水平速度v0=20m/s抛出,小球刚好落到斜面的底端B(空气阻力不计),求小球在平抛运动过程中离开斜面的最大高度.
如图所示,一小球自倾角θ=37°的斜面顶端A以水平速度v0=20m/s抛出,小球刚好落到斜面的底端B(空气阻力不计),求小球在平抛运动过程中离开斜面的最大高度. 如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求:
如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求: 如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )
如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )