题目内容
如图所示,在光滑、固定的水平杆上套着一个光滑的滑环m,滑环下通过一根不可伸长的轻绳悬吊一重物M,轻绳长为L,将滑环固定在水平杆上,给M一个水平冲量作用,使M摆动,且恰好刚碰到水平杆,求:

(1)M在摆动过程中,滑环对水平杆的压力的最大值是多少?
(2)若滑环m不固定,仍给M以同样大小的冲量作用,则M摆起的最大高度为多少?
解析:
设计意图:本题考查了圆周运动的知识应用以及机械能守恒的知识. 解析:(1)滑环固定时,M在摆动过程中机械能守恒,M刚好碰到杆时,即M到达最高时速度为0,设M在冲量I作用下获得的初速度为v0,由机械能守恒:
解得: M通过最低点时,绳中张力T最大,此时滑环对杆的压力也最大,由圆周运动知识得: T-Mg=M 解得:T=3Mg 再对滑环进行受力分析,此时滑环对杆的压力满足:FN=T+mg= (3M+m)g. (2)若滑环不固定,当M摆到最大高度时,其速度的竖直分量为0,此时M与滑环具有相同的速度v,在相同冲量作用下,M的初速度仍为
由动量守恒定律有: M 由①②联立得: H=m 所以H= 易错点:当环不固定时,M与环构成在水平方向上系统动量守恒,若该点分析不清则易错,同时另一点也应注意,即相同冲量作用于同一物体,其获得的速度一致. 答案:(1)T=3 Mg (2)H= |

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 如图所示,在光滑的水平面上停放一上表面水平的平板车C,C质量为3m,在车上左端放有质量为2m木块B,车左端靠于固定在竖直平面内半径为R的
如图所示,在光滑的水平面上停放一上表面水平的平板车C,C质量为3m,在车上左端放有质量为2m木块B,车左端靠于固定在竖直平面内半径为R的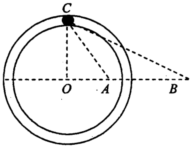 如图所示,在光滑绝缘水平面上固定着-根光滑绝缘的圆形水平渭槽,其圆心在O点.过O点的-条直径上的A、B两点固定着两个点电荷.其中固定于A点的为正电荷,电荷量大小为Q;固定于B点的是未知电荷.在它们形成的电场中,有-个可视为质点的质量为m、电荷量大小为q的带电小球正在滑槽中运动,小球的速度方向平行于水平面,若已知小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,AB间的距离为L,∠ABC=∠ACB=30°,CO⊥OB,静电力常量为k,
如图所示,在光滑绝缘水平面上固定着-根光滑绝缘的圆形水平渭槽,其圆心在O点.过O点的-条直径上的A、B两点固定着两个点电荷.其中固定于A点的为正电荷,电荷量大小为Q;固定于B点的是未知电荷.在它们形成的电场中,有-个可视为质点的质量为m、电荷量大小为q的带电小球正在滑槽中运动,小球的速度方向平行于水平面,若已知小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,AB间的距离为L,∠ABC=∠ACB=30°,CO⊥OB,静电力常量为k,
 圆弧形光滑轨道,已知轨道底端切线与水C上表面等高,另一物块质量为m的A从轨道顶端由静上释放,与B碰后立即粘于一体为D,在平板车C上滑行,并与固定于C右端水平轻质弹簧作用后被弹回,最后D刚好回到车的最左端与C相对静止,重力加速度为g,设AB碰撞时间极短,A、B均视为质点. 求:
圆弧形光滑轨道,已知轨道底端切线与水C上表面等高,另一物块质量为m的A从轨道顶端由静上释放,与B碰后立即粘于一体为D,在平板车C上滑行,并与固定于C右端水平轻质弹簧作用后被弹回,最后D刚好回到车的最左端与C相对静止,重力加速度为g,设AB碰撞时间极短,A、B均视为质点. 求: