题目内容
如图，AB为竖直半圆轨道的竖直直径，轨道半径R=10m，轨道A端与水平面相切．光滑木块从水平面上以一定初速度滑上轨道，若木块经B点时，对轨道的压力恰好为零，g取10m/s2，求：（1）小球经B点时的速度大小；
（2）小球落地点到A点的距离．
分析：（1）木块经B点时，对轨道的压力恰好为零，轨道对木块没有弹力，仅由重力提供木块做圆周运动所需要的向心力，由牛顿第二定律列式求解B点时的速度．
（2）木块离开B点后做平抛运动，由运动分解与合成的知识解决落地点到A点的距离．
（2）木块离开B点后做平抛运动，由运动分解与合成的知识解决落地点到A点的距离．
解答：解：（1）木块经B点时，仅由重力提供木块做圆周运动所需要的向心力，则有
mg=m
解得，v=10m/s
（2）木块离开B点后做平抛运动，则有
水平方向，有：
s=vt
竖直方向，有：
2R=
gt2
联立得s=20m
答：
（1）木块经B点时的速度大小是10m/s；
（2）木块落地点到A点的距离是20m．
mg=m
| v2 |
| R |
解得，v=10m/s
（2）木块离开B点后做平抛运动，则有
水平方向，有：
s=vt
竖直方向，有：
2R=
| 1 |
| 2 |
联立得s=20m
答：
（1）木块经B点时的速度大小是10m/s；
（2）木块落地点到A点的距离是20m．
点评：本题主要考查了向心力公式及平抛运动基本公式的直接应用，难度不大．
练习册系列答案
相关题目
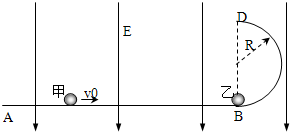如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段为半径R=0.2m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×103V/m．一不带电的绝缘小球甲，以速度v0沿水平轨道向右运动，与静止在B点带正电的小球乙发生弹性碰撞． 已知甲、乙两球的质量均为m=1.0×10-2kg，乙所带电荷量q=2.0×10-5C，g取10m/s2．（水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移）
如图，ABCD为竖直平面内的光滑绝缘轨道，其中AB段是倾斜的，倾角为37°，BC段是水平的，CD段为半径R=0.15m的半圆，三段轨道均光滑连接，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×103 V/m．一带正电的导体小球甲，在A点从静止开始沿轨道运动，与静止在C点不带电的相同导体小球乙发生弹性碰撞，碰撞后速度交换（即碰后甲的速度变成碰前瞬间乙的速度，乙的速度变成碰前瞬间甲的速度）．已知甲、乙两球的质量均为m=1.0×10-2㎏，小球甲所带电荷量为q甲=2.0×10-5C，g取10m/s2，假设甲、乙两球可视为质点，并不考虑它们之间的静电力，且整个运动过程与轨道间无电荷转移．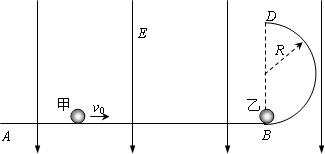
如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段为半径R=0.2m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×103V/m．一不带电的绝缘小球甲，以速度υ0沿水平轨道向右运动，与静止在B点带正电的小球乙发生弹性碰撞．已知甲、乙两球的质量均为m=1.0×10-2kg，乙所带电荷量q=2.0×10-5C，g取10m/s2．（水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移）
如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段是半径为R的半圆，两段轨道相切于B点．小球甲以速度υ0沿水平轨道向右运动，与静止在B点的小球乙发生弹性碰撞．已知甲、乙两球的质量均为m．（水平轨道足够长，甲、乙两球可视为质点）