Question

某校一课外活动小组自制一枚火箭，设火箭发射后始终在垂直于地面的方向上运动．火箭点火后可认为做匀加速直线运动，经过4 s到达离地面40 m高处时燃料恰好用完，若不计空气阻力，取g＝10 m/s²，求：

(1)燃料恰好用完时火箭的速度；

(2)火箭上升离地面的最大高度；

(3)火箭从发射到残骸落回地面过程的总时间．

 

Answer 1

【答案】

设燃料用完时火箭的速度为v₁，所用时间为t₁.火箭的上升运动分为两个过程，第一个过程为做匀加速上升运动，第二个过程为做竖直上抛运动至到达最高点．

(1)对第一个过程有h₁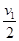＝t₁，代入数据解得v₁＝20 m/s.

(2)对第二个过程有h₂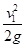＝，代入数据解得h₂＝20 m

所以火箭上升离地面的最大高度h＝h₁＋h₂＝40 m＋20 m＝60 m.

(3)方法一　分段分析法

从燃料用完到运动至最高点的过程中，由v₁＝gt₂得

t₂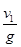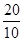＝＝ s＝2 s

从最高点落回地面的过程中，h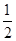＝gt₃²，而h＝60 m，代入得t₃＝2 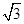s

故总时间t_总＝t₁＋t₂＋t₃＝(6＋2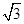) s.

方法二　整体分析法

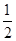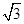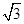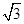考虑火箭从燃料用完到落回地面的全过程，以竖直向上为正方向，全过程为初速度v₁＝20 m/s、加速度g＝－10 m/s²、位移h＝－40 m的匀变速直线运动，即有h＝v₁t－ gt²，代入数据解得t＝(2＋2) s或t＝(2－2 ) s(舍去)，故t_总＝t₁＋t＝(6＋2 ) s.

【解析】本题考查匀变速公式的推论，对于匀变速直线运动，平均速度为V/2，考查了竖直上抛运动的最大高度公式，分阶段考虑的能力，竖直上抛运动整体上可按匀减速直线运动来处理