题目内容
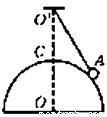
如图所示，重为G的小球A，用一根长为L的细绳悬吊起来放在半径为R的光滑固定球面上，由悬点O′到球面的最短距离O′C=s，问：（1）小球对球面的压力为多大？
（2）细线的拉力为多大？
【答案】分析：以小球为研究对象，分析小球的分力情况，根据共点力的平衡条件，由几何关系可得出小球受支持力和细线的拉力； 由牛顿第三定律可得出小球对球面的压力．
解答：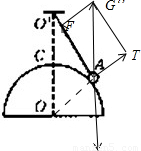
解：对小球受力分析如图所示：由图可知，小球受力中的△ATG'≌△OAO′，则有：
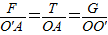
小球受到的支持力F=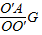
=
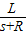G；
由牛顿第三定律可得，小球对球面的压力为F'=F=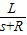
G
细线的拉力为T'=T=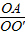
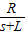G=
G；
答：（1）小球对球面的压力为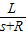
G；
（2）细线对小球的拉力为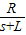
G．
点评：本题考查共点力的平衡条件的应用，注意几何关系应由相似三角形求出．
思考：若O'有一半径非常小的定滑轮，在拉动绳子使小球A向上滑动的过程中，分析二力的变化．
解答：
解：对小球受力分析如图所示：由图可知，小球受力中的△ATG'≌△OAO′，则有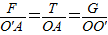：小球受到的支持力F=
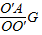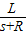=G； 由牛顿第三定律可得，小球对球面的压力为F'=F=
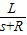G细线的拉力为T'=T=
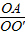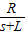G=G； 答：（1）小球对球面的压力为
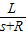G； （2）细线对小球的拉力为
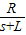G．点评：本题考查共点力的平衡条件的应用，注意几何关系应由相似三角形求出．
思考：若O'有一半径非常小的定滑轮，在拉动绳子使小球A向上滑动的过程中，分析二力的变化．
练习册系列答案
相关题目
如图所示，重为G的球放在倾角为θ的光滑斜面上，被竖直放置的光滑挡板挡住．若将挡板逐渐放低，则斜面对球的作用力F1和挡板对球的作用力F2的变化情况是（ ）
（2012?浦东新区一模）如图所示，重为G的匀质直角三角形薄板ABC，AB边长为L，∠BAC=θ，A为光滑的固定转动轴．现用垂直于AB边的力F作用在B端，使薄板的AB边处于水平方向且平衡，则三角形薄板的重心距离转动轴A的水平距离为
（2013?潍坊一模）如图所示，重为G的光滑球在倾角为θ的斜面和竖直墙壁之间处于静止状态．若将斜面换成材料和质量相同，但倾角θ稍小一些的斜面，以下判断正确的是（ ）
（2013?闵行区二模）如图所示，重为G的圆盘与一轻杆相连，杆与圆盘恰相切，支点为O．现用始终竖直向下的力F拉杆的另一端，使该端缓慢向下转动，则杆转到竖直之前，拉力F及其力矩M的变化情况是（ ）