Question

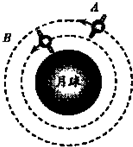假设发射两颗探月卫星A和B，如图所示，其环月飞行距月球表面的高度分别为200km和100km．若两颗卫星质量相同，环月运行均可视为匀速圆周运动，则（　　）

A．B环月运行时向心加速度比A大

B．B环月运行的速度比A大

C．B环月运行的周期比A大

D．B环月运行时机械能比A小

Answer 1

分析：卫星绕月球做圆周运动时，万有引力提供向心力，由牛顿第二定律列方程，求出向心加速度、线速度、周期表达式，然后分析答题．

解答：解：A、设卫星的质量为m、轨道半径为r、月球质量为M，
嫦娥卫星绕月球做匀速圆周运动，万有引力提供向心力得，

GMm

r2

=m

v2

r

=ma=m

4π2r

T2

A、向心加速度a=

GM

r2

，卫星A的轨道半径大于B的轨道半径，所以B环月运行时向心加速度比A大，故A正确
B、v=

GM r

，卫星A的轨道半径大于B的轨道半径，所以B环月运行的速度比A大，故B正确
C、周期T=2π

r3 GM

，卫星A的轨道半径大于B的轨道半径，所以B环月运行的周期比A小，故C错误
D、卫星的引力势能E_P=-

GMm

r

，动能E_k=

1

2

mv²=

GMm

2r

，
机械能E=E_P+E_k=-

GMm

2r

，所以B环月运行时机械能比A小，故D正确
故选ABD．

点评：本题关键抓住万有引力提供向心力，先列式求解出加速度、线速度、周期的表达式，再进行讨论．