题目内容
（单选）如图所示，水平桌面由粗糙程度不同的AB、BC两部分组成，且AB=BC，小物块P（可视为质点）以某一初速度从A点滑上桌面，最后恰好停在C点，已知物块经过AB与BC两部分的时间之比为1：4，则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为（P物块在AB、BC上所做的运动均可看作匀变速直线运动）（ ）分析：设到达B点速度为v1，先根据AB与BC段的位移相等并运用平均速度公式得到B点的速度；然后求解出AB与BC段的加速度，最后根据牛顿第二定律求解出AB、BC部分之间的动摩擦因数μ1、μ2之比．
解答：解：设到达B点速度为v1，由于AB与BC段的位移，有：
?t1=
?t2
其中：t1：t2=1：4
故：v1=
AB段的加速度为：a1=
=-
BC段的加速度为：a2=
=-
根据牛顿第二定律，有：
AB段：-μ1mg=ma1
BC段：-μ2mg=ma2
解得：μ1：μ2=a1：a2=8：1
故选：D．
| v0+v1 |
| 2 |
| v1+0 |
| 2 |
其中：t1：t2=1：4
故：v1=
| v0 |
| 3 |
AB段的加速度为：a1=
| v1-v0 |
| t1 |
| 2v0 |
| 3t1 |
BC段的加速度为：a2=
| 0-v1 |
| t2 |
| v0 |
| 3t2 |
根据牛顿第二定律，有：
AB段：-μ1mg=ma1
BC段：-μ2mg=ma2
解得：μ1：μ2=a1：a2=8：1
故选：D．
点评：本题关键是先根据平均速度公式求解出B点速度，得到加速度，然后结合牛顿第二定律列式求解动摩擦因素之比．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
（1）利用“油膜法估测分子直径”实验体现了构建分子模型的物理思想，也体现了通过对宏观量的测量来实现对微观量的间接测量方法．某同学在本实验中测得体积为V的油滴，落在平静的水面上，扩展成面积为S的单分子油膜，则该分子的直径为
（选修3-3模块）
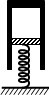，弹簧一端固定于水平面上，另一端与质量为m的活塞拴接在一起，开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体．气缸和活塞均可与外界进行热交换．若外界环境的温度缓慢降低，则封闭气体的体积将
，大气压强
，物重50N，活塞质量及一切摩擦不计，缓慢升高环境温度，使活塞刚好升到缸口，封闭气体吸收了60J的热量，则封闭气体的压强将 （选填“增加”、“减小”或“不变”），气体内能变化量为 J。
），现取一滴体积仍为V的油酸溶液在滴在水面上，在水面上形成面积为S的单分子油膜，已知油酸的密度为
，摩尔质量为M。请据此推算阿伏伽德罗常数的表达式。