题目内容
如图所示,竖直平面上的两个半径相同的光滑的半圆形轨道,分别处在沿水平方向的匀强电场和匀强磁场中,两个相同的带正电小球同时从两轨道左端最高点由静止释放.M、N为轨道的最低点,下列判断正确的是( )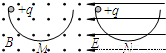
A.两小球到达轨道最低点的速度一定是vM>vN
B.两小球经过轨道最低点时对轨道的压力一定是NM>NN
C.小球第一次到达M点的时间大于小球第一次到达N点的时间
D.在磁场中小球能到达轨道的另一端最高处,在电场中小球不能到达轨道另一端最高处
【答案】分析:带电小球在磁场中运动,洛伦兹力不做功,根据动能定理求出运动到最低点的速度,从而根据牛顿第二定律求出底部对小球的支持力大小,然后进行比较.
解答:解:小球在磁场中运动,在最低点进行受力分析可知:
NM-mg-Bqv1=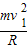
解得:NM=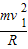 +mg+Bqv1…①
+mg+Bqv1…①
小球在电场中运动,在最低点受力分析可知:
NN-mg=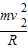
解得:NN=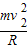 +mg…②
+mg…②
A、C、由于小球在磁场中运动,磁场力对小球不做功,整个过程中小球的机械能守恒;而小球在电场中运动受到的电场力对小球做负功,到达最低点时的速度的大小较小,所以在电场中运动的时间也长,故A正确,C错误;
B、因为v1>v2,结合①②可知:NM>NN,故B正确;
D、若在磁场中小球能运动到另一端的最高处,则根据动能定理知,在电场中,电场力始终做负功,小球不能到达最高点.故D正确.
故选ABD.
点评:解决本题的关键知道电场力做功和洛伦兹力做功的区别,知道洛伦兹力不做功,综合动能定理和牛顿第二定律进行求解.
解答:解:小球在磁场中运动,在最低点进行受力分析可知:
NM-mg-Bqv1=
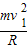
解得:NM=
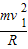 +mg+Bqv1…①
+mg+Bqv1…①小球在电场中运动,在最低点受力分析可知:
NN-mg=
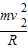
解得:NN=
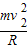 +mg…②
+mg…②A、C、由于小球在磁场中运动,磁场力对小球不做功,整个过程中小球的机械能守恒;而小球在电场中运动受到的电场力对小球做负功,到达最低点时的速度的大小较小,所以在电场中运动的时间也长,故A正确,C错误;
B、因为v1>v2,结合①②可知:NM>NN,故B正确;
D、若在磁场中小球能运动到另一端的最高处,则根据动能定理知,在电场中,电场力始终做负功,小球不能到达最高点.故D正确.
故选ABD.
点评:解决本题的关键知道电场力做功和洛伦兹力做功的区别,知道洛伦兹力不做功,综合动能定理和牛顿第二定律进行求解.

练习册系列答案
相关题目


 为多少时,C与B点的水平距离s最大,最大值是多少?
为多少时,C与B点的水平距离s最大,最大值是多少?

 为多少时,C与B点的水平距离s最大,最大值是多少?
为多少时,C与B点的水平距离s最大,最大值是多少?