题目内容
一个质量为m、电荷量为e的电子，以初速度v与电场线平行束射入匀强电场，经时间t电子具有的电势能与刚进入电场时相同，则此电场的场强大小为 ，电子在时间t内的运动路程为 ．
【答案】分析：由题，电子以初速度v与电场线平行束射入匀强电场，经时间t电子具有的电势能与刚进入电场时相同，速度大小相等，说明电子在匀强电场中做有往复的匀变速直线运动，根据对称性，往返时间相等．根据牛顿第二定律和速度公式结合，求出场强．由平均速度公式求出电子匀减速运动的位移大小，再求解路程．
解答：解：电子经过时间t时，初末时刻电势能相同，则电场力不做功、初末位置和速度都相同，电子在电场中一直作匀减速运动．从进入到速度减为0所用时间为t1=
，则有v=at1．
根据牛顿第二定律得，a=
，
得到v=at1=
，解得，E=
通过位移为s=
=
；电子在电场中的运动路程为S=2s=
．
故答案为：
，
．
点评：本题关键是分析电子的运动情况，此题也可以根据动量定理求解电场强度．
解答：解：电子经过时间t时，初末时刻电势能相同，则电场力不做功、初末位置和速度都相同，电子在电场中一直作匀减速运动．从进入到速度减为0所用时间为t1=
，则有v=at1．根据牛顿第二定律得，a=
，得到v=at1=
，解得，E=通过位移为s=
=；电子在电场中的运动路程为S=2s=．故答案为：
，．点评：本题关键是分析电子的运动情况，此题也可以根据动量定理求解电场强度．
练习册系列答案
相关题目
（2013?湛江一模）如图所示，竖直平行直线为匀强电场的电场线，电场方向未知，一个质量为m、电荷量为q的带负电粒子以初速度v0从A点垂直电场方向进入电场，该带电粒子经过电场中的B点和C点，不考虑带电粒子的重力．
如图所示，直角三角形的斜边倾角为30°．底边BC长为2L，处在水平位置，斜边AC是光滑绝缘的．在底边中点O点处放置一正电荷Q，一个质量为m，电荷量为q的带负电的质点从斜面顶端沿斜边滑下，滑到斜边上的垂足D时速度为v．试求真空中有一个电荷量为Q的点电荷固定不动．另一个质量为m，电荷量为-q的质点（其重力可忽略不计），在点电荷Q对它库仑力的作用下，绕Q作半径为r、周期为T的匀速圆周运动．
试证明：
=
．
试证明：
| r3 |
| T2 |
| kqQ |
| 4π2m |
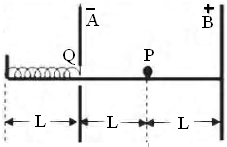如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的正、负电荷，在两板间形电场强度大小为E匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔中有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为q（q＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．一自然长度为L的轻弹簧左端固定在距A板左侧L处挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小球，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经过一段时间第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的
如图所示，在地面上方的水平匀强电场中，一个质量为m、电荷量为+q的小球，系在一根长为L的绝缘细线一端，可以在竖直平面内绕O点做圆周运动．AB为圆周的水平直径，CD为竖直直径．已知重力加速度为g，电场强度E=| mg |
| q |
A、若小球在竖直平面内绕O点做圆周运动，则它运动的最小速度为
| ||
| B、若小球在竖直平面内绕O点做圆周运动，则小球运动到B点时的机械能最大 | ||
| C、若将小球在A点由静止开始释放，它将在ACBD圆弧上往复运动 | ||
D、若将小球在A点以大小为
|