题目内容
如图所示,用特殊材料制成的PQ界面垂直于x轴,只能让垂直打到PQ界面上的电子通过.PQ的左右两侧有两个对称的直角三角形区域,左侧的区域内分布着方向垂直纸面向里、磁感应强度为B的匀强磁场,右侧区域内分布着竖直向上匀强电场.现有速率不同的电子在纸面上从坐标原点O沿不同方向射向三角形区域,不考虑电子间的相互作用.已知电子的电量为e,质量为m,在△OAC中,OA=l,θ=60°.
(1)求能通过PQ界面的电子所具有的最大速度及其从O点入射时与y轴的夹角;
(2)若以最大速度通过PQ界面的电子刚好被位于x轴上的F处的接收器所接收,求电场强度E;
(3)在满足第(2)问的情况下,求所有能通过PQ界面的电子最终穿过x轴的区间宽度.

(1)求能通过PQ界面的电子所具有的最大速度及其从O点入射时与y轴的夹角;
(2)若以最大速度通过PQ界面的电子刚好被位于x轴上的F处的接收器所接收,求电场强度E;
(3)在满足第(2)问的情况下,求所有能通过PQ界面的电子最终穿过x轴的区间宽度.

分析:(1)由题意,要使电子能通过PQ界面,电子飞出磁场的速度方向必须水平向右,电子运动的半径最大,对应的速度最大,由几何知识求出最大半径,即可求得电子的最大速度,并由数学知识求出电子从O点入射时与y轴的夹角.
(2)以最大速度通过PQ界面的电子进入电场后做类平抛运动,刚好被位于x轴上的F处的接收器所接收,水平位移为
l,竖直位移为l,由牛顿第二定律和运动学公式求解E.
(3)电子进入电场后做类平抛运动,出电场后做匀速直线运动穿过x轴,设类平抛运动的水平分位移为x1,竖直分位移为y1,出电场时速度的方向与水平方向的夹角为β,出电场后做匀速直线运动的水平分位移为x2,其轨迹与x轴的交点与PQ界面的距离为s.根据类平抛运动的规律和数学知识求解.
(2)以最大速度通过PQ界面的电子进入电场后做类平抛运动,刚好被位于x轴上的F处的接收器所接收,水平位移为
| 3 |
(3)电子进入电场后做类平抛运动,出电场后做匀速直线运动穿过x轴,设类平抛运动的水平分位移为x1,竖直分位移为y1,出电场时速度的方向与水平方向的夹角为β,出电场后做匀速直线运动的水平分位移为x2,其轨迹与x轴的交点与PQ界面的距离为s.根据类平抛运动的规律和数学知识求解.
解答:解: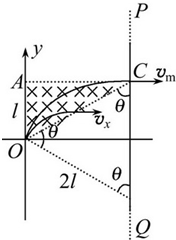 (1)要使电子能通过PQ界面,电子飞出磁场的速度方向必须水平向右.
(1)要使电子能通过PQ界面,电子飞出磁场的速度方向必须水平向右.
由Bev=m
可知,轨迹半径 r=
,r越大v越大,从C点水平飞出的电子,运动半径最大,对应的速度最大,即r=2l时,电子的速度最大,故最大速度为 vm=
,其从O点入射时与y轴夹角为30°.
(2)以最大速度通过PQ界面的电子进入电场后做类平抛运动,刚好被位于x轴上的F处的接收器所接收,则在电场中,有:
l=vmt,
l=
at2
又 a=
解得E=
(3)电子进入电场后做类平抛运动,出电场后做匀速直线运动穿过x轴,设类平抛运动的水平分位移为x1,竖直分位移为y1,出电场时速度的方向与水平方向的夹角为β,出电场后做匀速直线运动的水平分位移为x2,其轨迹与x轴的交点与PQ界面的距离为s.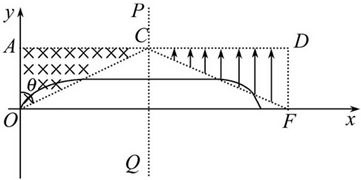
tan30°=
,
又根据类平抛运动的规律得:x1=vt,y1=
at2,a=
可得x1=
,tanβ=
=
,x2=
故 s=(
l-
r)+x1+x2=
l-
+
,其中0≤v≤vm
当v=
时,smin=
l
当v=0(或v=vm)时,smax=
l
所以所有能通过PQ界面的电子最终穿过x轴的区间宽度为smax-smin=
l-
l=
l
答:
(1)能通过PQ界面的电子所具有的最大速度是
,其从O点入射时与y轴的夹角是30°;
(2)若以最大速度通过PQ界面的电子刚好被位于x轴上的F处的接收器所接收,电场强度E是
.
(3)所有能通过PQ界面的电子最终穿过x轴的区间宽度为
l.
 (1)要使电子能通过PQ界面,电子飞出磁场的速度方向必须水平向右.
(1)要使电子能通过PQ界面,电子飞出磁场的速度方向必须水平向右.由Bev=m
| v2 |
| r |
| mv |
| qB |
| 2Bel |
| m |
(2)以最大速度通过PQ界面的电子进入电场后做类平抛运动,刚好被位于x轴上的F处的接收器所接收,则在电场中,有:
| 3 |
l=
| 1 |
| 2 |
又 a=
| eE |
| m |
解得E=
| 8B2el |
| 3m |
(3)电子进入电场后做类平抛运动,出电场后做匀速直线运动穿过x轴,设类平抛运动的水平分位移为x1,竖直分位移为y1,出电场时速度的方向与水平方向的夹角为β,出电场后做匀速直线运动的水平分位移为x2,其轨迹与x轴的交点与PQ界面的距离为s.

tan30°=
| y1 |
| x1 |
又根据类平抛运动的规律得:x1=vt,y1=
| 1 |
| 2 |
| eE |
| m |
可得x1=
| 2mv2 | ||
|
| at |
| v |
| 2 | ||
|
| ||
| tanβ |
故 s=(
| 3 |
| ||
| 2 |
| 3 |
| ||
| 4eB |
| ||
| 8B2e2l2 |
当v=
| vm |
| 2 |
7
| ||
| 8 |
当v=0(或v=vm)时,smax=
| 3 |
所以所有能通过PQ界面的电子最终穿过x轴的区间宽度为smax-smin=
| 3 |
7
| ||
| 8 |
| ||
| 8 |
答:
(1)能通过PQ界面的电子所具有的最大速度是
| 2Bel |
| m |
(2)若以最大速度通过PQ界面的电子刚好被位于x轴上的F处的接收器所接收,电场强度E是
| 8B2el |
| 3m |
(3)所有能通过PQ界面的电子最终穿过x轴的区间宽度为
| ||
| 8 |
点评:本题考查分析较为复杂的磁场、电场与力学的综合题,关键能画出电子的运动轨迹,充分运用数学知识进行分析和求解.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图所示用某种透明材料制成一块等腰直角棱镜,其顶点为A、B、C,使光线从AB面入射,调整到入射角θ取某个特殊值,恰能使它射入棱镜后在AC面上满足全反射临界条件.试求此材料的折射率n的大小.
如图所示用某种透明材料制成一块等腰直角棱镜,其顶点为A、B、C,使光线从AB面入射,调整到入射角θ取某个特殊值,恰能使它射入棱镜后在AC面上满足全反射临界条件.试求此材料的折射率n的大小. 如图所示,A、B两球完全相同,分别浸没在水和水银的同一深度内,A、B球用同一种特殊的材料制作,当温度稍微升高时,球的体积明显地增大,如果水和水银的初温及缓慢升高后的末温都相同,且两球膨胀后体积也相等,两球也不再上升,则( )
如图所示,A、B两球完全相同,分别浸没在水和水银的同一深度内,A、B球用同一种特殊的材料制作,当温度稍微升高时,球的体积明显地增大,如果水和水银的初温及缓慢升高后的末温都相同,且两球膨胀后体积也相等,两球也不再上升,则( ) (2009?深圳二模)如图所示,平行于直角坐标系y轴的PQ是用特殊材料制成的,只能让垂直打到PQ界面上的电子通过.其左侧有一直角三角形区域,分布着方向垂直纸面向里、磁感应强度为B的匀强磁场,其右侧有竖直向上场强为E的匀强电场.现有速率不同的电子在纸面上从坐标原点O沿不同方向射到三角形区域,不考虑电子间的相互作用.已知电子的电荷量为e,质量为m,在△OAC中,OA=a,θ=60°(即.∠AOC=60°)求:
(2009?深圳二模)如图所示,平行于直角坐标系y轴的PQ是用特殊材料制成的,只能让垂直打到PQ界面上的电子通过.其左侧有一直角三角形区域,分布着方向垂直纸面向里、磁感应强度为B的匀强磁场,其右侧有竖直向上场强为E的匀强电场.现有速率不同的电子在纸面上从坐标原点O沿不同方向射到三角形区域,不考虑电子间的相互作用.已知电子的电荷量为e,质量为m,在△OAC中,OA=a,θ=60°(即.∠AOC=60°)求: 在电喷汽车的进气管道中,广泛地使用着一种叫“电热丝式空气流量传感器”的部件,其核心部分是一种用特殊的合金材料制作的电热丝.如图所示,当进气管道中的冷空气流速越大时,电阻R两端的电压U0就变得越高,反之,电压U0就越低.这样,管道内空气的流量就转变成了可以测量的电压信号,便于汽车内的电脑系统实现自动控制,如果将这种电热丝从汽车的进气管道中取出,放在实验室中测量这种电热丝的伏安特性曲线,得到结果正确的是( )
在电喷汽车的进气管道中,广泛地使用着一种叫“电热丝式空气流量传感器”的部件,其核心部分是一种用特殊的合金材料制作的电热丝.如图所示,当进气管道中的冷空气流速越大时,电阻R两端的电压U0就变得越高,反之,电压U0就越低.这样,管道内空气的流量就转变成了可以测量的电压信号,便于汽车内的电脑系统实现自动控制,如果将这种电热丝从汽车的进气管道中取出,放在实验室中测量这种电热丝的伏安特性曲线,得到结果正确的是( )