Question

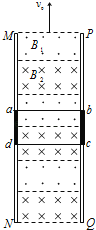
【题目】某工厂在竖直平面内安装了如图所示的传送装置，圆心为O的光滑圆弧轨道AB与足够长倾斜传送带BC在B处相切且平滑连接，OA连线水平、OB连线与竖直线的夹角为θ＝37°，圆弧的半径为R=1.0m，在某次调试中传送带以速度v =2m/s顺时针转动，现将质量为m1=3kg的物块P（可视为质点）从A点位置静止释放，经圆弧轨道冲上传送带，当物块P刚好到达B点时，在C点附近某一位置轻轻地释放一个质量为m2=1kg的物块Q在传送带上，经时间t=1.2s后与物块P相遇并发生碰撞，碰撞后粘合在一起成为粘合体S。已知物块P、Q、粘合体S与传送带间的动摩擦因数均为μ＝0.5，重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8。试求：

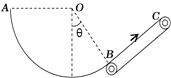
（1）物块P在B点的速度大小；

（2）传送带BC两端距离的最小值；

（3）粘合体回到圆弧轨道上B点时对轨道的压力。

Answer 1

【答案】(1) (2) (3)

【解析】（1）由A到B，对物块P由动能定理有：

可得物块P在B点的速度大小

（2）因vB>v，物块P在传送带上减速，受到向下的摩擦力，由牛顿第二定律有

可得物块P的加速度大小a1=10m/s2

减速至v的时间

运动位移

因x1<L，摩擦力反向，又因，物块P继续向上减速，有

可得物块P的加速度大小a2=2m/s2

减速至0的时间

因t2=t-t1，说明物块P刚好减速到零时与物块Q相遇发生碰撞

物块P第二段减速的位移大小

对物体Q：

可得其加速度a3=2m/s2

下滑的位移

BC的最小距离L=x1+x2+x3=3.04m

（3）碰撞前物体Q的速度v2=a3t=2.4m/s

物体P和Q碰撞： m2v2=(m1+m2)v3

可得碰撞后速度v3=0.6m/s

碰撞后粘合体以加速度a3向下加速运动，到圆弧上的B点的过程，有

可得粘合体在B点的速度v4=2.6m/s

在B点由牛顿第二定律有

可得轨道对粘合体的支持力F=59.04N

由牛顿第三定律得：粘合体S对轨道的压力F′=59.04N方向沿OB向下