题目内容
2. 如图所示,有一光滑、不计电阻且较长的“Ⅱ“型平行金属导轨,间距L=l m,导轨所在的平面与水平面的倾角为θ=37°,导轨空间内存在垂直导轨平面的匀强磁场.现将一质量m=0.1kg、电阻R=2Ω的金属杆水平靠在导轨上(与导轨两边垂直,且接触良好),g=l0m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,有一光滑、不计电阻且较长的“Ⅱ“型平行金属导轨,间距L=l m,导轨所在的平面与水平面的倾角为θ=37°,导轨空间内存在垂直导轨平面的匀强磁场.现将一质量m=0.1kg、电阻R=2Ω的金属杆水平靠在导轨上(与导轨两边垂直,且接触良好),g=l0m/s2,sin37°=0.6,cos37°=0.8.求:(1)若磁感应强度随时间变化满足B=2+0.2t(T),金属杆由距导轨顶部L1=l m处释放,求至少经过多长时间释放,会获得沿斜面向上的加速度;
(2)若匀强磁场大小为定值,对金属杆施加一个平行于导轨斜面向下的外力F,其大小为F=v+0.4(N),v为金属杆运动的速度,使金属杆以恒定的加速度a=10m/s2沿导轨向下做匀加速运动,求匀强磁场磁感应强度的大小;
(3)若磁感应强度随时间变化满足B=$\frac{2}{0.1+0.1{t}^{2}}$(T),t=0时刻金属杆从离导轨顶端L1=l m处静止释放,同时对金属杆施加一个外力,使金属杆沿导轨下滑且没有感应电流产生,求金属杆下滑L2=5m所用的时间.
分析 (1)金属杆有沿着斜面向上的加速度,此时安培力等于重力沿斜面的分力,根据共点力的平衡条件结合安培力的计算公式求解;
(2)由牛顿第二定律和安培力的计算公式求解磁感应强度大小;
(3)当磁通量保持不变时,感应电流为零,根据磁通量的定义式列方程求解.
解答 解:(1)金属杆有沿着斜面向上的加速度,此时安培力等于重力沿斜面的分力,则:FA=mgsinθ,
而安培力FA=BIL,
根据闭合电路的欧姆定律可得:I=$\frac{E}{R}$,
根据法拉第电磁感应定律可得:E=$\frac{△Φ}{△t}=\frac{△BL{L}_{1}}{△t}$,
联立解得:t=20s;
(2)由牛顿第二定律可得:F+mgsinθ-FA1=ma,
安培力FA1=B1I1L=$\frac{{B}_{1}^{2}{L}^{2}v}{R}$,
解得:B1=$\sqrt{2}T$≈1.4T;
(3)当磁通量保持不变时,感应电流为零,即Φ=Φ0,
根据磁通量的定义式可得:Φ0=B0LL1,Φ=BL(L1+L2),
解得:t2=$\sqrt{5}s$=2.24s.
答:(1)至少经过20s释放,会获得沿斜面向上的加速度;
(2)匀强磁场磁感应强度的大小为1.4T;
(3)金属杆下滑L2=5m所用的时间为2.24s.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
20. 如图所示,将一均匀导线围成一圆心角为90°的扇形导线框OMN,其中OM=R,线框总电阻为r,圆弧MN的圆心为O点,将导线框的O点置于直角坐标系的原点,其中第二和第四象限存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,第三象限存在垂直纸面向外的匀强磁场,磁感应强度大小为2B.从t=0时刻开始,让导线框以O点为圆心,以恒定的角速度ω沿逆时针方向做匀速圆周运动,则线框中的电流有效值为( )
如图所示,将一均匀导线围成一圆心角为90°的扇形导线框OMN,其中OM=R,线框总电阻为r,圆弧MN的圆心为O点,将导线框的O点置于直角坐标系的原点,其中第二和第四象限存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,第三象限存在垂直纸面向外的匀强磁场,磁感应强度大小为2B.从t=0时刻开始,让导线框以O点为圆心,以恒定的角速度ω沿逆时针方向做匀速圆周运动,则线框中的电流有效值为( )
 如图所示,将一均匀导线围成一圆心角为90°的扇形导线框OMN,其中OM=R,线框总电阻为r,圆弧MN的圆心为O点,将导线框的O点置于直角坐标系的原点,其中第二和第四象限存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,第三象限存在垂直纸面向外的匀强磁场,磁感应强度大小为2B.从t=0时刻开始,让导线框以O点为圆心,以恒定的角速度ω沿逆时针方向做匀速圆周运动,则线框中的电流有效值为( )
如图所示,将一均匀导线围成一圆心角为90°的扇形导线框OMN,其中OM=R,线框总电阻为r,圆弧MN的圆心为O点,将导线框的O点置于直角坐标系的原点,其中第二和第四象限存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,第三象限存在垂直纸面向外的匀强磁场,磁感应强度大小为2B.从t=0时刻开始,让导线框以O点为圆心,以恒定的角速度ω沿逆时针方向做匀速圆周运动,则线框中的电流有效值为( )| A. | $\frac{Bω{R}^{2}}{2r}$ | B. | $\frac{3Bω{R}^{2}}{2r}$ | C. | $\frac{2Bω{R}^{2}}{r}$ | D. | $\frac{\sqrt{5}Bω{R}^{2}}{2r}$ |
7. 应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.人坐在摩天轮吊厢的座椅上,摩天轮在竖直平面内按顺时针做匀速圆周运动的过程中,始终保持椅面水平,且人始终相对吊厢静止.关于人从最低点a随吊厢运动到最高点c的过程中,下列说法中正确的是( )
应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.人坐在摩天轮吊厢的座椅上,摩天轮在竖直平面内按顺时针做匀速圆周运动的过程中,始终保持椅面水平,且人始终相对吊厢静止.关于人从最低点a随吊厢运动到最高点c的过程中,下列说法中正确的是( )
 应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.人坐在摩天轮吊厢的座椅上,摩天轮在竖直平面内按顺时针做匀速圆周运动的过程中,始终保持椅面水平,且人始终相对吊厢静止.关于人从最低点a随吊厢运动到最高点c的过程中,下列说法中正确的是( )
应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.人坐在摩天轮吊厢的座椅上,摩天轮在竖直平面内按顺时针做匀速圆周运动的过程中,始终保持椅面水平,且人始终相对吊厢静止.关于人从最低点a随吊厢运动到最高点c的过程中,下列说法中正确的是( )| A. | 人始终处于超重状态 | B. | 座椅对人的摩擦力越来越大 | ||
| C. | 座椅对人的弹力越来越小 | D. | 人所受的合力始终不变 |
7.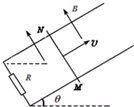 如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )
 如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨与水平面的夹角为θ,下端接有定值电阻R,匀强磁场垂直于导轨平面向上,磁感应强度为B.现给导体棒MN一平行于导轨的初速度v,使导体棒保持与导轨垂直并沿导轨向上运动,经过一段时间导体棒又回到原位置.不计导轨和导体棒的电阻,在这一过程中,下列说法正确的是( )| A. | 导体棒上滑时棒中的电流方向由N到M | |
| B. | 导体棒上滑阶段和下滑阶段受到的安培力方向相同 | |
| C. | 导体棒回到原位置时速度大小必小于v | |
| D. | 导体棒上滑阶段和下滑阶段的最大加速度大小相等 |
14. 如图所示,在0≤x≤2L的区域内存在着垂直于纸面向里的匀强磁场,磁感应强度大小为B,粗细均匀的正方形金属线框abcd位于xOy平面内,线框的bc边与x轴重合,cd边与y轴重合,线框的边长为L,总电阻为R.现让线框从图示位置由静止开始沿x轴正方向以加速度a做匀加速运动,则下列说法正确的是( )
如图所示,在0≤x≤2L的区域内存在着垂直于纸面向里的匀强磁场,磁感应强度大小为B,粗细均匀的正方形金属线框abcd位于xOy平面内,线框的bc边与x轴重合,cd边与y轴重合,线框的边长为L,总电阻为R.现让线框从图示位置由静止开始沿x轴正方向以加速度a做匀加速运动,则下列说法正确的是( )
 如图所示,在0≤x≤2L的区域内存在着垂直于纸面向里的匀强磁场,磁感应强度大小为B,粗细均匀的正方形金属线框abcd位于xOy平面内,线框的bc边与x轴重合,cd边与y轴重合,线框的边长为L,总电阻为R.现让线框从图示位置由静止开始沿x轴正方向以加速度a做匀加速运动,则下列说法正确的是( )
如图所示,在0≤x≤2L的区域内存在着垂直于纸面向里的匀强磁场,磁感应强度大小为B,粗细均匀的正方形金属线框abcd位于xOy平面内,线框的bc边与x轴重合,cd边与y轴重合,线框的边长为L,总电阻为R.现让线框从图示位置由静止开始沿x轴正方向以加速度a做匀加速运动,则下列说法正确的是( )| A. | 进入磁场时,线框中的电流沿abcda方向,出磁场时,线框中的电流沿adcba方向 | |
| B. | 进入磁场时,a端电势比b端电势高,出磁场时,b端电势比a端电势高 | |
| C. | a、b两端的电压最大值为$\frac{3}{4}$BL$\sqrt{aL}$ | |
| D. | 线框中的最大电功率为$\frac{6a{B}^{2}{L}^{3}}{R}$ |
11. 一平行板电容器中存在匀强电场,电场沿竖直方向,两个比荷(即粒子的电荷量与质量之比)不同的带电粒子a和b,从电容器边缘同一竖直线上的不同位置(如图)沿相同的水平方向同时射入两平行板之间,经过相同时间两粒子落在电容器下板同一点P上,若不计重力和粒子间的相互作用力,则下列说法正确的是( )
一平行板电容器中存在匀强电场,电场沿竖直方向,两个比荷(即粒子的电荷量与质量之比)不同的带电粒子a和b,从电容器边缘同一竖直线上的不同位置(如图)沿相同的水平方向同时射入两平行板之间,经过相同时间两粒子落在电容器下板同一点P上,若不计重力和粒子间的相互作用力,则下列说法正确的是( )
 一平行板电容器中存在匀强电场,电场沿竖直方向,两个比荷(即粒子的电荷量与质量之比)不同的带电粒子a和b,从电容器边缘同一竖直线上的不同位置(如图)沿相同的水平方向同时射入两平行板之间,经过相同时间两粒子落在电容器下板同一点P上,若不计重力和粒子间的相互作用力,则下列说法正确的是( )
一平行板电容器中存在匀强电场,电场沿竖直方向,两个比荷(即粒子的电荷量与质量之比)不同的带电粒子a和b,从电容器边缘同一竖直线上的不同位置(如图)沿相同的水平方向同时射入两平行板之间,经过相同时间两粒子落在电容器下板同一点P上,若不计重力和粒子间的相互作用力,则下列说法正确的是( )| A. | 粒子a的比荷大于粒子b | |
| B. | 粒子a射入时的初速度大于粒子b | |
| C. | 若只减小两板间的电压,则两粒子可能同时落在电容器下板边缘上 | |
| D. | 若只增大粒子b射入时的初速度,则两粒子可能在两板之间的某一位置相遇 |
 如图所示,一个上下都与大气相通的直圆筒,中间用两个活塞A与B堵住一定质量的理想气体,活塞面积为0.01m2,A与B都可沿圆筒无摩擦地上下滑动,但不漏气,A的质量为M=10kg,B的质量为m=0.5kg,B与一劲度系数为K=l000N/m较长的弹簧相连,已知大气压强为P0=1.0×l05Pa,平衡时两活塞间的距离l0=39cm.现用力压A,使A缓慢向下移动一段距离后再次平衡,此时用于压A的力F=200N.求活塞A向下移动的距离.(假定气体温度保持不变,B活塞未到下方通气孔,g取l0rn/s2)
如图所示,一个上下都与大气相通的直圆筒,中间用两个活塞A与B堵住一定质量的理想气体,活塞面积为0.01m2,A与B都可沿圆筒无摩擦地上下滑动,但不漏气,A的质量为M=10kg,B的质量为m=0.5kg,B与一劲度系数为K=l000N/m较长的弹簧相连,已知大气压强为P0=1.0×l05Pa,平衡时两活塞间的距离l0=39cm.现用力压A,使A缓慢向下移动一段距离后再次平衡,此时用于压A的力F=200N.求活塞A向下移动的距离.(假定气体温度保持不变,B活塞未到下方通气孔,g取l0rn/s2) 如图所示,一束单色光从半圆形玻璃砖的左侧平面MN上的A点垂直平面射入,半圆形玻璃砖的半径为R,OA=$\frac{1}{2}$R,一足够长的光屏平放在半圆形玻璃砖右侧与玻璃砖的对称轴重合,玻璃砖对该单色光的折射率为$\sqrt{3}$,求:
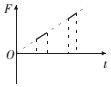
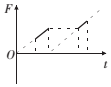
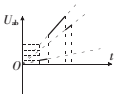
如图所示,一束单色光从半圆形玻璃砖的左侧平面MN上的A点垂直平面射入,半圆形玻璃砖的半径为R,OA=$\frac{1}{2}$R,一足够长的光屏平放在半圆形玻璃砖右侧与玻璃砖的对称轴重合,玻璃砖对该单色光的折射率为$\sqrt{3}$,求: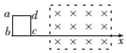 如图所示,abcd为边长为L的正方形线框,线框在纸面内,电阻为R.图中虚线区域内有垂直纸面向里的匀强磁场.现用外力作用于线框,使线框从图示位置开始沿x轴正方向做初速度为零的匀加速运动,线框运动过程中,ad边始终水平,线框平面始终与磁场垂直,磁场宽度大于L,以x轴正方向作为力的正方向,则磁场对线框的作用力F随时间t的变化图线及线框ab边的带你Uab随时间t的变化图象正确的是( )
如图所示,abcd为边长为L的正方形线框,线框在纸面内,电阻为R.图中虚线区域内有垂直纸面向里的匀强磁场.现用外力作用于线框,使线框从图示位置开始沿x轴正方向做初速度为零的匀加速运动,线框运动过程中,ad边始终水平,线框平面始终与磁场垂直,磁场宽度大于L,以x轴正方向作为力的正方向,则磁场对线框的作用力F随时间t的变化图线及线框ab边的带你Uab随时间t的变化图象正确的是( )