题目内容
一质点t=0时位于坐标原点，右图为该质点做直线运动的速度一时间图线，由图可知，
（1）在时间t=______ s时质点距坐标原点最远；
（2）从t=0到t=20s内通过的路程是______．
解：（1）在0～10s内，质点从原点出发向正方向做匀减速直线运动，10s末速度为零；在10～20s内，质点为沿负方向返回做匀加速直线运动．则10s末质点离坐标原点最远．
（2）由图质点在前10s内的位移大小为x1=
=20m．在后10s内的位移大小为x2=20m．则从t=0到t=20s内通过的路程是40m．
故本题答案是：10；40m
分析：根据速度图象分析质点的运动情况，确定什么时刻质点离坐标原点最远．分析“面积”分别求出前10s和后10s内位移的大小，再求解总路程．
点评：本题考查根据速度图象分析质点运动情况的能力，注意位移与路程的区别．
（2）由图质点在前10s内的位移大小为x1=
=20m．在后10s内的位移大小为x2=20m．则从t=0到t=20s内通过的路程是40m．故本题答案是：10；40m
分析：根据速度图象分析质点的运动情况，确定什么时刻质点离坐标原点最远．分析“面积”分别求出前10s和后10s内位移的大小，再求解总路程．
点评：本题考查根据速度图象分析质点运动情况的能力，注意位移与路程的区别．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
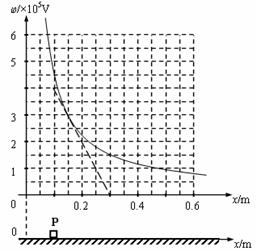
粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势j与坐标值x的关系如下表格所示：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
根据上述表格中的数据可作出如右的j—x图像。现有一质量为0.10kg，电荷量为1.0´10-7C带正电荷的滑块（可视作质点），其与水平面的动摩擦因数为0.20。问：
（1）由数据表格和图像给出的信息，写出沿x轴的电势j与x的函数关系表达式。
（2）若将滑块无初速地放在x=0.10m处，则滑块最终停止在何处？
（3）在上述第（2）问的整个运动过程中，它的加速度如何变化？当它位于x=0.15m时它的加速度多大？（电场中某点场强为φ-t图线上某点对应的斜率）
（4）若滑块从x=0.60m处以初速度v0沿-x方向运动，要使滑块恰能回到出发点，其初速度v0应为多大？
，AB是一条直径，今有一束平行光沿AB方向射向圆柱体，试求：