题目内容
如图所示，在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷，将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力．若小球所带电荷量很小，不影响O点处的点电荷的电场，则放于圆心处的电荷在AB弧中点处的电场强度大小（ ）
A．E=
| B．E=
| C．E=
| D．E=
|
设细管的半径为R，小球到达B点时速度大小为v．小球从A滑到B的过程，由机械能守恒定律得：
mgR=
mv2
得到：v=
小球经过B点时，由牛顿第二定律得：
Eq-mg=m
将v=
代入得：
E=
根据点电荷电场强度可知，圆心处的电荷在AB弧中点处的电场强度大小也为E=
．
故选D
mgR=
| 1 |
| 2 |
得到：v=
| 2gR |
小球经过B点时，由牛顿第二定律得：
Eq-mg=m
| v2 |
| R |
将v=
| 2gR |
E=
| 3mg |
| q |
根据点电荷电场强度可知，圆心处的电荷在AB弧中点处的电场强度大小也为E=
| 3mg |
| q |
故选D
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
如图所示，在竖直放置的光滑半圆弧绝缘细管的圆心O处固定一点电荷，将质量为m，带电量为+q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力．求：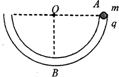
如图所示，在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷，将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无作用力．若小球所带电荷量很小，不影响O点处的点电荷的电场，则放于圆心O处的点电荷在OB连线的中点处的电场强度大小（ ）
如图所示，在竖直放置的半圆形容器的中心O点分别以水平速度v1，v2抛出两个小球（可视为质点），最终它们分别落在圆弧上的A点和B点，已知OA与OB相互垂直且OA与竖直方向成a角，求两小球初速度之比v1，：v2．
如图所示，在竖直放置的光滑绝缘的半圆形细管的圆心O处放一点电荷，将质量为m、带电量为q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力，则放于圆心处的电荷在AB弧中点处的电场强度大小为（ ）
（2012?东城区三模）如图所示，在竖直放置的金属板M上放一个放射源C，可向纸面内各个方向射出速率均为v的α粒子，P是与金属板M平行的足够大的荧光屏，到M的距离为d．现在P与金属板M间加上垂直纸面的匀强磁场，调整磁感应强度的大小，恰使沿M板向上射出的α粒子刚好垂直打在荧光屏上．若α粒子的质量为m，电荷量为+2e．则（ ）