题目内容
如图所示，在粗糙水平面上有两个质量分别为m1和m2的木块1和2，中间用一原长为L，劲度系数为k的轻弹簧连接，木块与地面之间的摩擦因数为μ，现用一水平力向右拉木块2，使两木块一起匀速运动，下列说法中正确的是（ ）分析：当两木块一起匀速运动时，木块1受到重力、弹簧的拉力、地面的支持力和摩擦力而平衡，根据平衡条件求出弹簧的弹力，由胡克定律求出弹簧伸长的长度，再求解两木块之间的距离．
解答：解：A、对木块1研究．木块1受到重力、弹簧的拉力、地面的支持力和摩擦力．
根据平衡条件弹簧的弹力FN=μm1g
又由胡克定律得到弹簧伸长的长度x=
=
所以两木块一起匀速运动时两木块之间的距离是：
S=L+x=L+
m1g．故A正确B错误；
C、刚撤去拉力F时，由于弹簧没来得及发生形变，则弹簧的弹力来不及改变，则1的受力情况不变，加速度仍为0，而2受力F消失，则此时受弹簧拉力和摩擦力的合力为F=μ（m1+m2）g
根据牛顿第二定律，则2的加速度a=
=
，故C错误D正确；
故选：AD．
根据平衡条件弹簧的弹力FN=μm1g
又由胡克定律得到弹簧伸长的长度x=
| FN |
| K |
| μm1g |
| k |
S=L+x=L+
| μ |
| k |
C、刚撤去拉力F时，由于弹簧没来得及发生形变，则弹簧的弹力来不及改变，则1的受力情况不变，加速度仍为0，而2受力F消失，则此时受弹簧拉力和摩擦力的合力为F=μ（m1+m2）g
根据牛顿第二定律，则2的加速度a=
| F |
| m2 |
| μg(m1+m2) |
| m2 |
故选：AD．
点评：本题是平衡条件和胡克定律的综合应用，关键是选择研究对象，分析物体的受力情况．
练习册系列答案
相关题目
（2006?潍坊一模）如图所示，在粗糙水平面上放一质量为M的斜面，质量为m的木块在竖直向上力F作用下，沿斜面匀速下滑，此过程中斜面保持静止，则地面对斜面（ ）
如图所示，在粗糙水平面上依次放有两块质量分别为m2=15kg，m3=10kg高度完全相同的木板A、B，质量m1=20kg的货物C与木板间的动摩擦因数为μ1，木板A与地面间的动摩擦因数μ2=0.3，木板B与地面间的动摩擦因数μ3=0.2．（最大静摩擦力与滑动摩擦力大小相等，取g=10m/s2）要使货物C滑上木板时，木板A不动，而滑上木板B时，木板B开始滑动，则μ1的大小可能是（ ）
如图所示，在粗糙水平面上固定点电荷Q，在M点无初速释放带电小物块，小物块运动到N点时静止，则从M点运动到N点的过程中（ ）| A、小物块所受电场力逐渐增大 | B、小物块具有的电势能逐渐增大 | C、M点的电势可能高于N点的电势 | D、小物块电势能变化量的大小一定等于克服摩擦力做的功 |
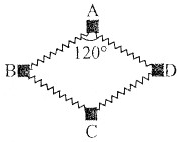如图所示，在粗糙水平面上放置A、B、C、D四个小物块，各小物块之间由四根完全相同的轻弹簧相互连接，正好组成一个菱形，∠BAD=120°，整个系统保持静止状态．已知A物块所受的摩擦力大小为f，则D物块所受的摩擦力大小为（ ）A、
| ||||
| B、f | ||||
C、
| ||||
| D、2 f |
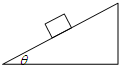如图所示，在粗糙水平面上有一个倾角为θ的斜面体，斜面上放着一个质量为m的物块，物块与斜面体间的动摩擦因素为μ，整个系统处于静止状态，则下列关于物块与斜面体之间的摩擦力及斜面体与水平地面的摩擦力说法正确的是（ ）| A、物块斜面体之的间摩擦力大小为μmgcosθ | B、水平地面对斜面体的摩擦力方向水平向右 | C、水平地面对斜面体的摩擦力方向水平向左 | D、斜面体与水平地面没有摩擦力的作用 |