题目内容
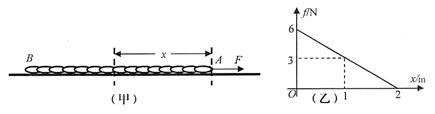
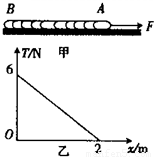一根质量分布均匀的长绳AB，在恒定水平外力F的作用下，沿光滑水平面做直线运动，如图甲所示．绳内距A端x处的张力T与x的关系如图乙所示，由图可知（ ）A．水平外力F=6N
B．绳子的质量m=3kg
C．绳子的长度2m
D．绳子的加速度2m/s2
【答案】分析：本题的关键是设出绳子总长度和总质量，求出单位长度，然后分别对绳子用整体法和隔离法受力分析，列出牛顿第二定律方程，求解即可．
解答：解：设绳总长为L，总质量为m，则绳单位长度质量为λ=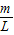
，先对整个绳子有F=ma，可得绳子加速度为a=
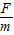，再对绳子左端部分应有T=λ（L-x）a，整理可得T=-
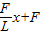，结合图象截距和斜率概念可知F=6N，
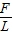=3，解得L=2m，所以A、C正确，无法求出绳子质量m大小，也无法求出加速度a的大小，故B、D错误．
故选AC．
点评：遇到连接体问题，一般是采用“先整体，后隔离”的分析方法，运算较简洁．
解答：解：设绳总长为L，总质量为m，则绳单位长度质量为λ=
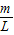，先对整个绳子有F=ma，可得绳子加速度为a=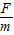，再对绳子左端部分应有T=λ（L-x）a，整理可得T=-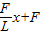，结合图象截距和斜率概念可知F=6N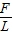，=3，解得L=2m，所以A、C正确，无法求出绳子质量m大小，也无法求出加速度a的大小，故B、D错误．故选AC．
点评：遇到连接体问题，一般是采用“先整体，后隔离”的分析方法，运算较简洁．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
2m／s的初速度做匀加速直线运动（忽略绳子的形变），在头2s内所通过的位移等于绳长的6倍。如图甲所示，绳内距A端x处的张力（即绳内部之间的拉力）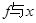
的关系如图乙所示，利用图象和题中的已知数据，求：
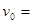2m／s的初速度做匀加速直线运动（忽略绳子的形变），在头2s内所通过的位移等于绳长的6倍。如图甲所示，绳内距A端x处的张力（即绳内部之间的拉力）
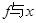的关系如图乙所示，利用图象和题中的已知数据，求：