��Ŀ����
16�� ijС��ˮ��վ�ĵ�������ʾ��ͼ��ͼ��ʾ�������ͨ����ѹ��ѹ��T1�ͽ�ѹ��ѹ��T2���û����磮��֪����ߵ��ܵ���ΪR����ѹ��ѹ��T2��ԭ������Ȧ����֮��Ϊ4��1����ѹ��ѹ������Ȧ���˽����ѹu=220$\sqrt{2}$ sin��100��t�� V����ѹ��ѹ���ĸ���Ȧ����ֵR0=11���ĵ�����ɱպϵ�·��������ѹ����Ϊ�����ѹ����������˵������ȷ���ǣ�������
ijС��ˮ��վ�ĵ�������ʾ��ͼ��ͼ��ʾ�������ͨ����ѹ��ѹ��T1�ͽ�ѹ��ѹ��T2���û����磮��֪����ߵ��ܵ���ΪR����ѹ��ѹ��T2��ԭ������Ȧ����֮��Ϊ4��1����ѹ��ѹ������Ȧ���˽����ѹu=220$\sqrt{2}$ sin��100��t�� V����ѹ��ѹ���ĸ���Ȧ����ֵR0=11���ĵ�����ɱպϵ�·��������ѹ����Ϊ�����ѹ����������˵������ȷ���ǣ�������| A�� | ͨ��R0��������Чֵ��20 A | |
| B�� | ��ѹ��ѹ��T2ԭ������Ȧ�ĵ�ѹ��Ϊ1��4 | |
| C�� | ��ѹ��ѹ��T1�������ѹ���ڽ�ѹ��ѹ��T2�������ѹ | |
| D�� | ��ѹ��ѹ��T1��������ʴ��ڽ�ѹ��ѹ��T2�����빦�� |
���� ���ݵ�ѹ�����������ȣ������������ɷ��ȣ�������ý�ѹ��ѹ���ĵ�����������ϵĵ����Ĵ�С���Ӷ������������ߺ��õ������ĵĹ��ʵĴ�С��
��� �⣺A����ѹ��ѹ������Ȧ���˽����ѹ��ЧֵΪ$\frac{220\sqrt{2}}{\sqrt{2}}=220V$�����ص���Ϊ11��������ͨ��R0��������Чֵ��$\frac{220}{11}=20A$��ѡ��A��ȷ��
B����ѹ��ѹ��T2��ԭ������Ȧ����֮��Ϊ4��1�����ݵ�ѹ�����������ȣ�����ѡ��B����
C����ѹ��ѹ��T1�������ѹ���ڽ�ѹ��ѹ��T2�������ѹ����������ϵĵ�ѹ������ѡ��C����
D����ѹ��ѹ��T1��������ʵ��ڽ�ѹ��ѹ��T2�����빦�ʼ���������ϵĹ��ʣ�����ѡ��D��ȷ��
��ѡ��AD��
���� ����ס�����ѹ���ĵ�ѹ������֮��Ĺ�ϵ�����ֵ����Чֵ֮��Ĺ�ϵ���ɽ�����⣮

��ϰ��ϵ�д�
�����Ŀ
6��ͼ1��ʾΪһ�м�г�Შ��t=0��ʱ�IJ���ͼ��ͼ2�����в���P�����ͼ�ߣ���ô�ò��Ĵ����ٶȺʹ��������ǣ�������


| A�� | ��=0.5m/s����x�Ḻ���� | B�� | ��=1m/s����x�Ḻ���� | ||
| C�� | ��=0.5m/s����x�������� | D�� | ��=1m/s����x�������� |
7�� ��ͼ��ij�ֻ��ij�����������ӵ�220V���е����ܸ��ֻ��ṩ5V�ij���ѹ��˵���ó�����ڵı�ѹ���ܹ���������
��ͼ��ij�ֻ��ij�����������ӵ�220V���е����ܸ��ֻ��ṩ5V�ij���ѹ��˵���ó�����ڵı�ѹ���ܹ���������
 ��ͼ��ij�ֻ��ij�����������ӵ�220V���е����ܸ��ֻ��ṩ5V�ij���ѹ��˵���ó�����ڵı�ѹ���ܹ���������
��ͼ��ij�ֻ��ij�����������ӵ�220V���е����ܸ��ֻ��ṩ5V�ij���ѹ��˵���ó�����ڵı�ѹ���ܹ���������| A�� | ���߽�����ѹ | B�� | ���ͽ�����ѹ | C�� | ����ֱ����ѹ | D�� | ����ֱ����ѹ |
11��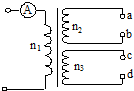 ��ͼ��ʾ����ѹ�������ѹUһ������������Ȧ�������ֱ�Ϊn2��n3�����ѵ���������a��b�ϣ�ʹc��d����ʱ��ͨ��ԭ��Ȧ�еĵ�������ʾ����I0������ͬһ����������c��d�ϣ�ʹa��b����ʱ����������ʾ��ΪI�䣬��$\frac{{I}_{0}}{I��}$Ϊ��������
��ͼ��ʾ����ѹ�������ѹUһ������������Ȧ�������ֱ�Ϊn2��n3�����ѵ���������a��b�ϣ�ʹc��d����ʱ��ͨ��ԭ��Ȧ�еĵ�������ʾ����I0������ͬһ����������c��d�ϣ�ʹa��b����ʱ����������ʾ��ΪI�䣬��$\frac{{I}_{0}}{I��}$Ϊ��������
 ��ͼ��ʾ����ѹ�������ѹUһ������������Ȧ�������ֱ�Ϊn2��n3�����ѵ���������a��b�ϣ�ʹc��d����ʱ��ͨ��ԭ��Ȧ�еĵ�������ʾ����I0������ͬһ����������c��d�ϣ�ʹa��b����ʱ����������ʾ��ΪI�䣬��$\frac{{I}_{0}}{I��}$Ϊ��������
��ͼ��ʾ����ѹ�������ѹUһ������������Ȧ�������ֱ�Ϊn2��n3�����ѵ���������a��b�ϣ�ʹc��d����ʱ��ͨ��ԭ��Ȧ�еĵ�������ʾ����I0������ͬһ����������c��d�ϣ�ʹa��b����ʱ����������ʾ��ΪI�䣬��$\frac{{I}_{0}}{I��}$Ϊ��������| A�� | n2��n3 | B�� | n3��n2 | C�� | n22��n32 | D�� | n32��n22 |
1�����й��ڹ����ʵ�˵����ȷ���ǣ�������
| A�� | ������ƽֱ��·����ʻʱ�ߵ�λһ���ȵ͵�λ�ٶȴ� | |
| B�� | ��ֹ�ڱ仯�ų��е���Ȧ�����ĸ�Ӧ�綯���Ǹ����糡�������Ľ�� | |
| C�� | �����и�Ÿ��߲�����Ӧ�綯������Ϊ�������������������ɵ������������� | |
| D�� | һ������õ�Ħ�������ܹ�����Ϊ����Ҳ����Ϊ�� |
8����֪����Kepler-186f�ƺ���Kepler452������Բ���˶���������ΪT1��ij������������ظ߶ȵ��ڵ���뾶��Բ�ι�����Ƶ���������Բ���˶���������ΪT2������Kepler452����������������֮��Ϊp������Kepler-186f�ƺ���Kepler452�˶��Ĺ���뾶�����뾶֮��Ϊq����T1��T2֮��Ϊ��������
| A�� | $\sqrt{\frac{{q}^{3}}{8p}}$ | B�� | $\sqrt{\frac{p}{8{q}^{3}}}$ | C�� | $\sqrt{\frac{{q}^{3}}{p}}$ | D�� | $\sqrt{\frac{p}{{q}^{3}}}$ |
6��������Щ����¿ɽ����忴���ʵ㣨������
| A�� | �о�ijѧ�������г��ؼҵ��ٶ� | |
| B�� | ��ijѧ�������г����ƽ��з��� | |
| C�� | �о�����̽�����ӵ����ǵķ����ٶ� | |
| D�� | �о��������ת |



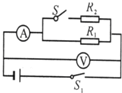 ��ͼ��ʾ����S�պ�ʱ����ѹ���͵���������Ϊ����������ʾ����Ϊ1.6V��0.4A����S�Ͽ�ʱ�����ǵ�ʾ����Ϊ1.7V��0.3A�����Դ�ĵ綯�ƣ�
��ͼ��ʾ����S�պ�ʱ����ѹ���͵���������Ϊ����������ʾ����Ϊ1.6V��0.4A����S�Ͽ�ʱ�����ǵ�ʾ����Ϊ1.7V��0.3A�����Դ�ĵ綯�ƣ�