题目内容
如图所示,一个小球从高h=10m处以水平速度v0=10m/s抛出,撞在倾角θ=45°的斜面上的P点,已知AC=5m,求:
(1)P、C之间的距离;
(2)小球撞击P点时速度的大小和方向.
(1)P、C之间的距离;
(2)小球撞击P点时速度的大小和方向.

(1)设P、C之间的距离为L,根据平抛运动规律,5+Lcos45°=v0t
h-Lsin45°=
gt2,
联立解得:L=5
m,t=1s.
(2)小球撞击P点时的水平速度v∥=v0=10m/s,
竖直速度vy=gt=10m/s.
小球撞击P点时速度的大小为v=
=10
m/s,
设小球的速度方向与水平方向的夹角为α,则tanα=
=1,α=45°,方向垂直于斜面向下.所以小球垂直于斜面向下撞击P点.
答:(1)P、C之间的距离是5
m;
(2)小球撞击P点时速度的大小是10
m/s,小球垂直于斜面向下撞击P点.
h-Lsin45°=
| 1 |
| 2 |
联立解得:L=5
| 2 |
(2)小球撞击P点时的水平速度v∥=v0=10m/s,
竖直速度vy=gt=10m/s.
小球撞击P点时速度的大小为v=
|
| 2 |
设小球的速度方向与水平方向的夹角为α,则tanα=
| vy |
| v0 |
答:(1)P、C之间的距离是5
| 2 |
(2)小球撞击P点时速度的大小是10
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一个小球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.在球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( )
如图所示,一个小球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.在球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( ) 如图所示,一个小球从D点竖直上抛到最高点A的频闪照片,不计空气阻力,则小球在D、B两点的速度之比vD:vB=
如图所示,一个小球从D点竖直上抛到最高点A的频闪照片,不计空气阻力,则小球在D、B两点的速度之比vD:vB= 如图所示,一个小球从半圆形轨道的A点的正上方80cm处的O点落下,恰好从A点进入轨道,到达B点.已知轨道的半径为30cm,求小球到达B点时的位移.
如图所示,一个小球从半圆形轨道的A点的正上方80cm处的O点落下,恰好从A点进入轨道,到达B点.已知轨道的半径为30cm,求小球到达B点时的位移.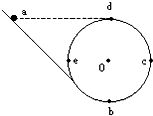 一个竖直放置的光滑圆环,半径为R,c、e、b、d分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图所示.一个小球从与d点高度相等的a点从斜轨上无初速下滑.试求:
一个竖直放置的光滑圆环,半径为R,c、e、b、d分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图所示.一个小球从与d点高度相等的a点从斜轨上无初速下滑.试求: