题目内容
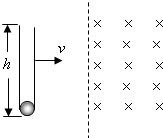 (2005?济南二模)如图所示,下端封闭,上端开口、高h=5m内壁光滑的细玻璃管竖直放置,管底有一质量m=10g、电荷量q=0.2c的小球.整个装置以v=5m/s的速度沿垂直于磁场方向进入B=0.2T、方向水平的匀强磁场,由于外力的作用,玻璃管在磁场中的速度保持不变,最终小球从上端管口飞出.取g=10m/s2.求:
(2005?济南二模)如图所示,下端封闭,上端开口、高h=5m内壁光滑的细玻璃管竖直放置,管底有一质量m=10g、电荷量q=0.2c的小球.整个装置以v=5m/s的速度沿垂直于磁场方向进入B=0.2T、方向水平的匀强磁场,由于外力的作用,玻璃管在磁场中的速度保持不变,最终小球从上端管口飞出.取g=10m/s2.求:(1)小球的电性
(2)小球在管中运动的时间
(3)小球在管中运动的过程中增加的机械能.
分析:(1)判断出小球所受洛伦兹力的方向,然后由左手定则判断出小球带什么电.
(2)小球在竖直方向上做匀加速直线运动,由牛顿第二定律求出小球的加速度,然后由位移公式求出小球的运动时间.
(3)由动能定理求出小球动能的增加量,由重力势能的计算公式求出重力势能的增加量,然后求出小球机械能的增加量.
(2)小球在竖直方向上做匀加速直线运动,由牛顿第二定律求出小球的加速度,然后由位移公式求出小球的运动时间.
(3)由动能定理求出小球动能的增加量,由重力势能的计算公式求出重力势能的增加量,然后求出小球机械能的增加量.
解答:解:(1)小球从管口上端飞出,则小球在玻璃管中所受洛伦兹力方向竖直向上,
由图示可知磁场垂直于纸面向里,小球沿水平方向向右运动,由左手定则可知,小球带正电.
(2)小球的实际运动速度可分解为水平方向的速度v和竖直方向的速度vy.
与两个分速度对应的洛伦兹力的分力分别是水平方向的Fx和竖直方向的Fy.其中,
竖直方向的洛伦兹力F=qvB不变,在竖直方向上,
由牛顿第二定律得:qvB-mg=ma,解得:a=10m/s2,
由匀变速运动的位移公式得:h=
at2,解得t=1s.
(3)小球飞出管口时,竖直速度为vy=at=10m/s,
飞出管口的合速度为v合=
=
=5
m/s,
动能增量△EK=
mv合2-
mv2=0.5J,
重力势能的增量△Ep=mgh=0.5J,
机械能的增量△E=△EK+△EP=1J;
答:(1)小球的电性为正.
(2)小球在管中运动的时间是1s;
(3)小球在管中运动的过程中增加的机械能为1J.
由图示可知磁场垂直于纸面向里,小球沿水平方向向右运动,由左手定则可知,小球带正电.
(2)小球的实际运动速度可分解为水平方向的速度v和竖直方向的速度vy.
与两个分速度对应的洛伦兹力的分力分别是水平方向的Fx和竖直方向的Fy.其中,
竖直方向的洛伦兹力F=qvB不变,在竖直方向上,
由牛顿第二定律得:qvB-mg=ma,解得:a=10m/s2,
由匀变速运动的位移公式得:h=
| 1 |
| 2 |
(3)小球飞出管口时,竖直速度为vy=at=10m/s,
飞出管口的合速度为v合=
|
| 102+52 |
| 5 |
动能增量△EK=
| 1 |
| 2 |
| 1 |
| 2 |
重力势能的增量△Ep=mgh=0.5J,
机械能的增量△E=△EK+△EP=1J;
答:(1)小球的电性为正.
(2)小球在管中运动的时间是1s;
(3)小球在管中运动的过程中增加的机械能为1J.
点评:分析清楚小球的运动过程,应用左手定则、牛顿第二定律、运动学公式、运动的合成、动能定理等即可正确解题.

练习册系列答案
相关题目
 (2005?济南二模)如图所示的电路中,L1、L2、L3、L4是四只相同的电灯,当滑动变阻器的滑片P向上滑动时,下列说法中正确的是( )
(2005?济南二模)如图所示的电路中,L1、L2、L3、L4是四只相同的电灯,当滑动变阻器的滑片P向上滑动时,下列说法中正确的是( ) (2005?济南二模)如图所示,把一个带正电的小球a放在光滑绝缘斜面上,欲使球a能静止在斜面上,需在MN间放一带电小球b,则b应:( )
(2005?济南二模)如图所示,把一个带正电的小球a放在光滑绝缘斜面上,欲使球a能静止在斜面上,需在MN间放一带电小球b,则b应:( )
 (2005?济南二模)二分频“音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混和音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动,如图为音箱的电路图,高、低频混和电流由a、b输入,L1和L2是线圈,C1和C2是电容器,则 ( )
(2005?济南二模)二分频“音箱内有两个不同口径的扬声器,它们的固有频率分别处于高音、低音频段,分别称为高音扬声器和低音扬声器,音箱要将扩音机送来的含有不同频率的混和音频电流按高、低频段分离出来,送往相应的扬声器,以便使电流所携带的音频信息按原比例还原成高、低频的机械振动,如图为音箱的电路图,高、低频混和电流由a、b输入,L1和L2是线圈,C1和C2是电容器,则 ( )