题目内容
如图是简化后的跳台滑雪的雪道示意图．整个雪道由倾斜的助滑雪道AB和着陆雪道DE，以及水平的起跳平台CD组成，AB与CD圆滑连接．运动员从助滑雪道AB上由静止开始，在重力作用下，滑到D点水平飞出，不计飞行中的空气阻力，经2s在水平方向飞行了60m，落在着陆雪道DE上．已知从B点到D点运动员的速度大小不变．（g取10m/s2 ）求：（1）运动员在AB段下滑到B点的速度大小；
（2）若不计阻力，运动员在AB段下滑过程中下降的高度
（3）若运动员的质量为60kg，他下滑到B点的速度大小为v1=20
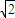m/s，他在AB段滑行过程克服阻力做了多少功？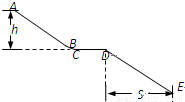
【答案】分析：（1）运动员从B点开始做的是平抛运动，根据人在水平方向上的运动可以求得平抛的初速度的大小，即为在AB段下滑到B点的速度大小；
（2）人在下滑的过程中，根据机械能守恒可以用求得下滑时的高度的大小；
（3）根据动能定理可以求得过程中人克服阻力所做的功．
解答：解：（1）已知从B点到D点运动员的速度大小不变．
运动员从D点飞出时的速度
v=
=30m/s
依题意，下滑到B点的速度大小是30 m/s
（2）下滑过程中机械能守恒，有
mgh=
mv2
下降的高度 h=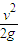
=45m
（3）由动能定理，有
mgh-Wf=
mv12
运动员克服阻力做功为：Wf=mgh-
mv12=3000 J
答：（1）运动员在AB段下滑到B点的速度大小是30m/s；
（2）若不计阻力，运动员在AB段下滑过程中下降的高度是45m
（3）若运动员的质量为60kg，他下滑到B点的速度大小为v1=20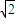
m/s，他在AB段滑行过程克服阻力做了3000 J 功．
点评：物体做平抛运动，我们可以把平抛运动可以分解为水平方向上的匀速直线运动，和竖直方向上的自由落体运动来求解，两个方向上运动的时间相同．
（2）人在下滑的过程中，根据机械能守恒可以用求得下滑时的高度的大小；
（3）根据动能定理可以求得过程中人克服阻力所做的功．
解答：解：（1）已知从B点到D点运动员的速度大小不变．
运动员从D点飞出时的速度
v=
=30m/s依题意，下滑到B点的速度大小是30 m/s
（2）下滑过程中机械能守恒，有
mgh=
mv2 下降的高度 h=
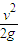=45m （3）由动能定理，有
mgh-Wf=
mv12运动员克服阻力做功为：Wf=mgh-
mv12=3000 J 答：（1）运动员在AB段下滑到B点的速度大小是30m/s；
（2）若不计阻力，运动员在AB段下滑过程中下降的高度是45m
（3）若运动员的质量为60kg，他下滑到B点的速度大小为v1=20
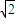m/s，他在AB段滑行过程克服阻力做了3000 J 功．点评：物体做平抛运动，我们可以把平抛运动可以分解为水平方向上的匀速直线运动，和竖直方向上的自由落体运动来求解，两个方向上运动的时间相同．
练习册系列答案
相关题目
（2008?广州模拟）如图是简化后的跳台滑雪的雪道示意图．整个雪道由倾斜的助滑雪道AB和着陆雪道CD，以及水平的起跳平台BC组成，AB与BC圆滑连接．运动员从助滑雪道AB上由静止开始下滑，到达C点后水平飞出，以后落到F点．E是运动轨迹上的某一点，在该点运动员的速度方向与轨道CD平行．设运动员从C到E与从E与F的运动时间分别为tCE和tEF，则它们的大小关系为（ ）
（2012?东城区一模）如图是简化后的跳台滑雪的雪道示意图．整个雪道由倾斜的助滑雪道AB和着陆雪道DE，以及水平的起跳平台CD组成，AB与CD圆滑连接．运动员从助滑雪道AB上由静止开始，在重力作用下，滑到D点水平飞出，不计飞行中的空气阻力，经2s在水平方向飞行了60m，落在着陆雪道DE上．已知从B点到D点运动员的速度大小不变．（g取10m/s2 ）求：
（2006?北京）如图是简化后的跳台滑雪的雪道示意图．整个雪道由倾斜的助滑雪道AB和着陆雪道DE，以及水平的起跳平台CD组成，AB与CD圆滑连接．运动员从助滑雪道AB上由静止开始，在重力作用下，滑到D点水平飞出，不计飞行中的空气阻力，经2s在水平方向飞行了60m，落在着陆雪道DE上，已知从B点到D点运动员的速度大小不变．（g取10m/s2）求
（2013?虹口区一模）如图是简化后的跳台滑雪的雪道示意图．整个雪道由倾斜的助滑雪道AB和着陆雪道CD，以及水平的起跳平台BC组成，AB与BC圆滑连接．运动员从助滑雪道AB上由静止开始下滑，到达C点后水平飞出，以后落到F点．E是运动轨迹上的某一点，在该点运动员的速度方向与轨道CD平行，E′点是E点在斜面上的垂直投影．设运动员从C到E与从E与F的运动时间分别为tCE和tEF．则关于tCE和tEF以及CE′和E′F的比例关系可能正确的是（ ）