题目内容
18.如图所示,小球甲从光滑斜面上高h=20cm的A点由静止释放以a=5m/s2的加速度下滑,同时小球乙从C点以速度v0沿光滑水平面向左匀速运动,C点与斜面底端B处的距离L=0.4m,甲滑下后能通过斜面底端的光滑小圆弧平稳地朝乙追去,甲释放后经过t=1s刚好追上乙,求乙的速度v0大小.(g取10m/s2)
分析 恰好追上表示经过相同的时间,甲乙两球到达同一位置,抓住位移之间的关系根据运动学基本公式即可求解.
解答 解:设小球甲在光滑斜面上运动的时间为t1,运动到B处时的速度为v1,从B处到追上小球乙所用时间为t2,则有:a=gsin θ=5 m/s2
解得 θ=30°
由$\frac{h}{sin30°}=\frac{1}{2}{at}_{1}^{2}$得:${t}_{1}=\sqrt{\frac{4h}{a}}=\frac{\sqrt{2}}{5}s$
v1=at1=$5×\frac{\sqrt{2}}{5}m/s$=$\sqrt{2}$ m/s
t2=t-t1=1-$\frac{\sqrt{2}}{5}$ s
v0t+L=v1t2
解得:${v}_{0}=\frac{{v}_{1}{t}_{2}-L}{t}=\frac{\sqrt{2}(1-\frac{\sqrt{2}}{5})-0.4}{1}m/s$=0.6m/s
答:小球乙的速度为 0.6 m/s.
点评 追击问题要注意抓住时间和位移,明确甲乙在水平面上的位移关系,运用运动学基本公式即可解题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
9.有两颗行星A、B,在这两颗行星表面附近各有一颗卫星绕行星做匀速圆周运动,若这两颗卫星运行的周期相等,则下列说法正确是( )
| A. | 两颗行星的半径相等 | B. | 两颗行星的密度相等 | ||
| C. | 两颗卫星的质量相等 | D. | 两颗卫星的线速度大小相等 |
13.电场强度E的定义式为E=$\frac{F}{q}$,下面说法中正确的是( )
| A. | 该定义只适用于点电荷产生的电场 | |
| B. | 库仑定律的表达式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$可以说是点电荷q2产生的电场在点电荷q1处的库仑力大小;而k$\frac{{q}_{1}}{{r}^{2}}$可以说是点电荷q2产生的电场在点电荷q1处的场强大小 | |
| C. | 对E=$\frac{F}{q}$,F是放入电场中的点电荷所受的静电力,q是产生电场的电荷的电荷量 | |
| D. | 电场中某点场强的方向与试探电荷的正负无关 |
3.一轮船以一定的速度垂直河流向对岸行驶,当河水匀速流动时,轮船所通过的路程、过河所用的时间与水流速度的正确关系是( )
| A. | 水速越大,路程越长,时间越长 | B. | 水速越大,路程越短,时间越短 | ||
| C. | 水速越大,路程和时间都不变 | D. | 水速越大,路程越长,时间不变 |
3.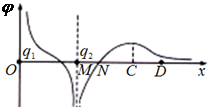 两电荷量分别为q1和q2的点电荷固定在x轴的原点O和坐标x0的M点,两电荷连线上各点电势φ随x变化的关系如图,其中ND段中坐标为2x0的C点电势最高.带负电的检验电荷从N点移到D点.下列判断正确的是( )
两电荷量分别为q1和q2的点电荷固定在x轴的原点O和坐标x0的M点,两电荷连线上各点电势φ随x变化的关系如图,其中ND段中坐标为2x0的C点电势最高.带负电的检验电荷从N点移到D点.下列判断正确的是( )
 两电荷量分别为q1和q2的点电荷固定在x轴的原点O和坐标x0的M点,两电荷连线上各点电势φ随x变化的关系如图,其中ND段中坐标为2x0的C点电势最高.带负电的检验电荷从N点移到D点.下列判断正确的是( )
两电荷量分别为q1和q2的点电荷固定在x轴的原点O和坐标x0的M点,两电荷连线上各点电势φ随x变化的关系如图,其中ND段中坐标为2x0的C点电势最高.带负电的检验电荷从N点移到D点.下列判断正确的是( )| A. | q1=2q2 | |
| B. | q1为正电荷,q2为负电荷 | |
| C. | 电场力对该检验电荷先做负功后做正功 | |
| D. | 该检验电荷到达C点时速度最大 |
20. Oxy坐标系中,将一电子从y轴上的a点移至x轴上的b点,需克服静电力做功W,若将一质子从y轴上的a点移至x轴上的c点,静电力做功为W,oa两点的距离为h,a、b、c三点的电势分别为φa、φb、φc,元电荷用e表示,不计重力,则下列说法中正确的是( )
Oxy坐标系中,将一电子从y轴上的a点移至x轴上的b点,需克服静电力做功W,若将一质子从y轴上的a点移至x轴上的c点,静电力做功为W,oa两点的距离为h,a、b、c三点的电势分别为φa、φb、φc,元电荷用e表示,不计重力,则下列说法中正确的是( )
 Oxy坐标系中,将一电子从y轴上的a点移至x轴上的b点,需克服静电力做功W,若将一质子从y轴上的a点移至x轴上的c点,静电力做功为W,oa两点的距离为h,a、b、c三点的电势分别为φa、φb、φc,元电荷用e表示,不计重力,则下列说法中正确的是( )
Oxy坐标系中,将一电子从y轴上的a点移至x轴上的b点,需克服静电力做功W,若将一质子从y轴上的a点移至x轴上的c点,静电力做功为W,oa两点的距离为h,a、b、c三点的电势分别为φa、φb、φc,元电荷用e表示,不计重力,则下列说法中正确的是( )| A. | φb>φc | |
| B. | φa<φb | |
| C. | 若空间中的电场是匀强电场,电场的方向沿y轴正方向 | |
| D. | 若空间中的电场是匀强电场,场强大小为E=$\frac{W}{eh}$ |
1.下列说法中正确的是( )
| A. | 一般情况下,交流电表测量的数值是交流电的瞬时值 | |
| B. | 穿过线圈的磁通量越大,感应电动势越大 | |
| C. | 由磁感应强度B=$\frac{F}{IL}$可知,当通电导体所受安培力变大时,其所在处磁感应强度B也变大 | |
| D. | 感应电流的磁场总要阻碍引起感应电流的磁通量的变化 |
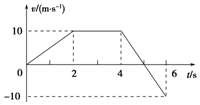 一物体自t=0时开始做直线运动,其速度图线如图所示,求:
一物体自t=0时开始做直线运动,其速度图线如图所示,求: