题目内容
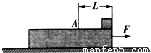
质量为m的足够长的木板放在光滑水平地面上，在木板的上表面的右端放一质量为m的小金属块（可看成质点），如图所示，木板上表面的A点右侧是光滑的，A点到木板右端距离为L，A点左侧表面与金属块间的动摩擦因数为μ．现用一个大小为F的水平拉力向右拉木板，当小金属块到达A点时立即撤去此拉力．求：（1）拉力F的作用时间是多少？
（2）最终木板的速度多大？
（3）小金属块到木板右端的最大距离为多少？
【答案】分析：（1）小金属块从开始运动到到达A点的过程中，由于没有摩擦力处于静止状态，而木板做匀加速运动，通过的位移为L，根据牛顿第二定律求木板的加速度，由运动学位移公式求时间．
（2）金属块到达A点时立即撤去拉力，此后系统所受的合外力为零，动量守恒，最终金属块与木板的速度相等．先由运动学公式求出小金属块到达A点时木板的速度，根据系统动量守恒求最终木板的速度．
（3）根据系统的能量守恒列式求出小金属块和木板相互摩擦的距离S，小金属块到木板右端的最大距离S总=S+L
解答：解：（1）开始时，小金属块静止，对木板进行研究，根据牛顿第二定律：
…①
设经时间t小金属块到达木板上表面的A点，则：
…②
联立①②解得：
…③
（2）当小金属块到达木板上表面的A点时，木板的速度为
…④，
此后小金属块和木板相互摩擦直至速度相等的过程中，动量守恒：mvl=（m+m）v2 …⑤
联立④⑤解得，最终木板的速度为：
…⑥
（3）小金属块和木板相互摩擦直至速度相等的过程能量守恒：
…⑦
联立④⑥⑦解得，小金属块和木板相互摩擦的距离
…⑧
小金属块到木板右端的最大距离
…⑨
答：（1）拉力F的作用时间是
．
（2）最终木板的速度
．
（3）小金属块到木板右端的最大距离为
．
点评：本题是滑块在木板上滑动的类型，要分过程进行研究，运用牛顿第二定律、运动学公式和动量守恒、机械能守恒进行求解．
（2）金属块到达A点时立即撤去拉力，此后系统所受的合外力为零，动量守恒，最终金属块与木板的速度相等．先由运动学公式求出小金属块到达A点时木板的速度，根据系统动量守恒求最终木板的速度．
（3）根据系统的能量守恒列式求出小金属块和木板相互摩擦的距离S，小金属块到木板右端的最大距离S总=S+L
解答：解：（1）开始时，小金属块静止，对木板进行研究，根据牛顿第二定律：
…①设经时间t小金属块到达木板上表面的A点，则：
…②联立①②解得：
…③（2）当小金属块到达木板上表面的A点时，木板的速度为
…④，此后小金属块和木板相互摩擦直至速度相等的过程中，动量守恒：mvl=（m+m）v2 …⑤
联立④⑤解得，最终木板的速度为：
…⑥（3）小金属块和木板相互摩擦直至速度相等的过程能量守恒：
…⑦联立④⑥⑦解得，小金属块和木板相互摩擦的距离
…⑧小金属块到木板右端的最大距离
…⑨答：（1）拉力F的作用时间是
．（2）最终木板的速度
．（3）小金属块到木板右端的最大距离为
．点评：本题是滑块在木板上滑动的类型，要分过程进行研究，运用牛顿第二定律、运动学公式和动量守恒、机械能守恒进行求解．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
（2011?湖南模拟）如图所示，足够长的水平传送带始终以v=3m/s的速度大小向左运动，传送带上有一质量为M=2kg、左侧面开口的小木盒A，A与传送带之间的动摩擦因数为μ=0.3，开始时，A与传送带之间保持相对静止．先后相隔△t=3s有两个质量m=1kg的光滑小球B自传送带的左端出发，以v0=15m/s的速度大小在传送带上向右运动．第1个球与木盒相遇后立即进入盒中且与盒粘合在一起获得方向向右的共同速度，这个相遇粘合的过程时间极短，损失的机械能△E=108J；第2个球出发后历时△t=
如图所示，足够长的水平传送带始终以v=3m/s的速度大小向左运动，传送带上有一质量为M=2kg、左侧面开口的小木盒A，A与传送带之间的动摩擦因数为μ=0.3，开始时，A与传送带之间保持相对静止．先后相隔△t=3s有两个质量m=1kg的光滑小球B自传送带的左端出发，以v0=15m/s的速度大小在传送带上向右运动．第1个球与木盒相遇后立即进入盒中且与盒粘合在一起获得方向向右的共同速度，这个相遇粘合的过程时间极短，损失的机械能△E=108J；第2个球出发后历时△t=
s而与木盒相遇．g取10m/s2．求：