题目内容
【题目】一个竖立着的轻弹簧，支撑着倒立的薄壁气缸（导热性能良好）的活塞使气缸静止，如图所示，此时环境温度为T0（单位K），封闭气柱的长度L1=30cm，气缸口未着地，当环境温度缓慢降为 
T0时，气缸正好着地，但与地面之间无压力，假设活塞与气缸壁之间无摩擦且不漏气，已知气缸质量M=10kg，活塞质量m=4kg，轻弹簧原长为27cm，活塞的横截面积S=2×10﹣3m2 ， 大气压强p0=1×105Pa，当地重力加速度g=10m/s2 ， 求：
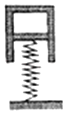
①环境温度为T0时气缸口离地高度h；
②当环境温度缓慢降为 
T0时，弹簧恰好恢复原长，求弹簧的劲度系数．
【答案】解：①气缸内气体发生等圧変化，根据盖﹣吕萨克定律有：
代入数据： 
解得： 
气缸下降的高度为： 
即环境温度为 
时气缸口离地高度为5cm
②气缸刚着地时气缸内气体的压强为 
，对气缸： 
= 
=1.5× 
弹簧恰好恢复原长时，以活塞为研究对象有： 
根据理想气体状态方程，有：
代入数据： 
= 
解得： 
=14.4cm
弹簧的形变量为： 
=10.6cm
活塞刚着地时，对活塞有： 
代入数据： 
= 
+k 
解得：k=1320N/m
答：①环境温度为T0时气缸口离地高度h为5cm；
②当环境温度缓慢降为 
T0时，弹簧恰好恢复原长，弹簧的劲度系数为1320N/m
【解析】气缸内的气体温度从缓慢降为
，气体发生等压变化，根据盖-吕萨克定律求末状态封闭气体的长度，气缸气柱的长度的差即为环境温度为T0时气缸口离地高度h；然后要求出气缸内气体在刚着地时的压强和最终弹簧恢复原长时的压强，根据理想气体状态方程求出弹簧恢复原长时气柱长度，求出弹簧的形变量，再根据活塞的受力平衡即可求出求出弹簧的劲度系数；本题关键是分析清楚气体状态变化过程、难点是选择恰当的研究对象进行受力分析求气体压强。
