题目内容
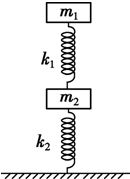 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
分析:系统原来处于平衡状态,两个弹簧均被压缩,弹簧k2的弹力等于两物体的总重力.缓慢向上提上面的木块,直到它刚离开上面弹簧时弹簧k2的弹力等于m2g,根据胡克定律分别求出下面弹簧两种状态下压缩的长度,下面木块移动的距离等于弹簧两种状态下压缩的长度之差.
解答:解:(1)m1离开弹簧后,下面弹簧的弹力大于F=m2g=k2△x,所以压缩量△x=
(2)设下面弹簧受到的弹力为F2,压缩量为△x2,上面弹簧受到的弹力为F1,压缩量为△x1,
由物体的平衡及胡克定律有:F2=(m1+m2)g,
△x2=
F1=m1g,△x1=
所以平衡时总长为L=L1+L2-△x1-△x2
=L1+L2-
-
.
当上面的物体刚离开时总长为L′=L1+L2-△x=L1+L2-
所以上面物体移动的距离△L=L′-L=
+
-
答:(1)m1离开弹簧后,下面弹簧的压缩量
;
(2)这个过程中上面木块移动的距离
+
-
| m2g |
| k2 |
(2)设下面弹簧受到的弹力为F2,压缩量为△x2,上面弹簧受到的弹力为F1,压缩量为△x1,
由物体的平衡及胡克定律有:F2=(m1+m2)g,
△x2=
| (m1+m2)g |
| k2 |
F1=m1g,△x1=
| m1g |
| k1 |
所以平衡时总长为L=L1+L2-△x1-△x2
=L1+L2-
| m1g |
| k1 |
| (m1+m2)g |
| k2 |
当上面的物体刚离开时总长为L′=L1+L2-△x=L1+L2-
| m2g |
| k2 |
所以上面物体移动的距离△L=L′-L=
| m1g |
| k1 |
| (m1+m2)g |
| k2 |
| m2g |
| k2 |
答:(1)m1离开弹簧后,下面弹簧的压缩量
| m2g |
| k2 |
(2)这个过程中上面木块移动的距离
| m1g |
| k1 |
| (m1+m2)g |
| k2 |
| m2g |
| k2 |
点评:对于弹簧问题,往往先分析弹簧原来的状态,再分析变化后弹簧的状态,找出物体移动距离与弹簧形变之间的关系.

练习册系列答案
相关题目
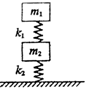 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的度系数分别为k1的k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这个过程中两木块m1和m2移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的度系数分别为k1的k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这个过程中两木块m1和m2移动的距离为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不栓接),整个系统处于平衡状态,现缓慢向上提上面的木块,直到它刚离开上面弹簧,求在这过程中下面木块移动的距离.
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不栓接),整个系统处于平衡状态,现缓慢向上提上面的木块,直到它刚离开上面弹簧,求在这过程中下面木块移动的距离. 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,两弹簧与两木块均连接在一起,整个系统处于平衡状态.现缓慢向上提上面弹簧的上端A,直到下面的木块m2刚离开地面.在此过程中上面弹簧的上端A移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,两弹簧与两木块均连接在一起,整个系统处于平衡状态.现缓慢向上提上面弹簧的上端A,直到下面的木块m2刚离开地面.在此过程中上面弹簧的上端A移动的距离为( ) 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,整个系统处于平衡状态,则k1,k2两轻质弹簧的形变量大小分别为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,整个系统处于平衡状态,则k1,k2两轻质弹簧的形变量大小分别为( )