题目内容
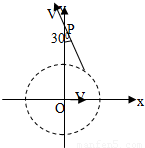 一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m,电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示.不计重力的影响.求磁场的磁感应强度B的大小及xy平面上磁场区域的半径R.
一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m,电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示.不计重力的影响.求磁场的磁感应强度B的大小及xy平面上磁场区域的半径R.
【答案】分析:一带电粒子,以一定的速度垂直进入匀强磁场中,由洛伦兹力提供向心力,使其做匀速圆周运动.根据入射点与出射点的速度方向可确定圆弧对应的圆心,由几何关系来确定磁场的磁感应强度B的大小及xy平面上磁场区域的半径R.
解答:解:粒子在磁场中受到洛伦兹力作用,做匀速圆周运动,则有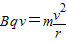
据此并由题意可得,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外.过P沿速度方向作延长线,它与x轴相交于Q点.作圆弧过O点与x轴相切,并且与PQ相切,切点A即粒子离开磁场区的地点.这样也求得圆弧轨迹的圆心C,
如图所示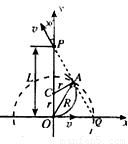
由图中几何关系得:L=3r
由以上两式可得: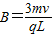
图中OA的长度即圆形磁场区的半径R,由图中几何关系可得
R=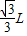
点评:带电粒子在磁场中由洛伦兹力提供做匀速圆周运动,同时结合数学几何关系来构建长度关系.注意运动圆弧的半径与磁场半径的区别.
解答:解:粒子在磁场中受到洛伦兹力作用,做匀速圆周运动,则有
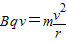
据此并由题意可得,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外.过P沿速度方向作延长线,它与x轴相交于Q点.作圆弧过O点与x轴相切,并且与PQ相切,切点A即粒子离开磁场区的地点.这样也求得圆弧轨迹的圆心C,
如图所示

由图中几何关系得:L=3r
由以上两式可得:
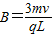
图中OA的长度即圆形磁场区的半径R,由图中几何关系可得
R=
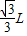
点评:带电粒子在磁场中由洛伦兹力提供做匀速圆周运动,同时结合数学几何关系来构建长度关系.注意运动圆弧的半径与磁场半径的区别.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





