题目内容
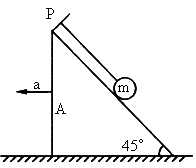
如图所示,一细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球.试求当滑块以a=2g的加速度向左运动时线中的拉力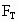 .
.
答案:略
解析:
解析:
|
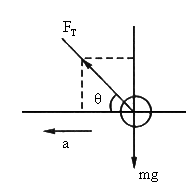
本题中当滑块向左运动的加速度较小时,滑块对小球存在支持力;当滑块向左运动的加速度较大时,小球将脱离滑块斜面而“飘”起来.因此,本题存在一个临界条件:当滑块向左运动的加速度为某一临界值时,斜面对小球的支持力恰好为零 (小球将要离开斜面而“飘”起来).我们首先求此临界条件.此时小球受两个力:重力mg;绳的拉力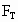 .根据牛顿第二定律的正交表示,有 .根据牛顿第二定律的正交表示,有
联立①、②两式并将代入,得 a=g ,即当斜面体滑块向左运动的加速度为 a=g时,小球恰好对斜面无压力.当 a>g时,小球将“飘”起来,当a=2g时,小球已“飘”起来了,此时小球的受力情况也正如图所示,故根据①、②两式并将a=2g代入,解得
此即为所求线中的拉力. 在本题的解析过程中,通过对临界条件的求解,可清楚看到,当 a>g时,绳与水平方向的夹角小于45°,且a越大,夹角θ越小(其极限值为:a→∞时θ→0).很多同学在求解此题时常犯下列错误:由方程①得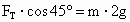 ,从而得 ,从而得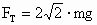 .实际上a=2g时球已离开斜面,线与水平方向的夹角不是45°了. .实际上a=2g时球已离开斜面,线与水平方向的夹角不是45°了.
另外,请读者思考一下,本题当系统向右、向下或向上做加速 (或减速)运动时,还可能会有哪些“临界条件”? |

练习册系列答案
相关题目
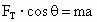
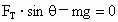
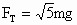
 如图所示,一细线的一端固定于倾角为30°的光滑楔形滑块A的顶端P处.细线的另一端拴一质量为m的小球,细线与斜面平行.当滑块至少以a=
如图所示,一细线的一端固定于倾角为30°的光滑楔形滑块A的顶端P处.细线的另一端拴一质量为m的小球,细线与斜面平行.当滑块至少以a= 如图所示,一小球质量为m,用长为L的细线悬于O点,在O点正下方
如图所示,一小球质量为m,用长为L的细线悬于O点,在O点正下方 如图所示,一细线的一端固定于倾角为45°的光滑楔型滑块A的顶端P处,细线的另一端拴一质量为m的小球,
如图所示,一细线的一端固定于倾角为45°的光滑楔型滑块A的顶端P处,细线的另一端拴一质量为m的小球,






















