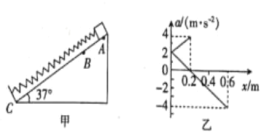
题目内容
【题目】如图所示,半径为r的半圆弧轨道ABC固定在竖直平面内,直径AC水平,一个质量为m的物块从圆弧轨道A端正上方P点由静止释放,物块刚好从A点无碰撞地进入圆弧轨道并做匀速圆周运动,到B点时对轨道的压力大小等于物块重力的2倍,重力加速度为g,不计空气阻力,不计物块的大小,则( )
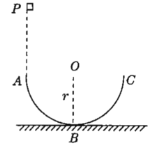
A.物块到达A点时速度大小为![]()
B.P、A间的高度差为![]()
C.物块从A运动到B所用时间为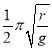
D.物块从A运动到B克服摩擦力做功为mgr
【答案】BCD
【解析】
A.在B点时由牛顿第二定律得
![]()
因为
![]()
所以
![]()
因为进入圆弧轨道做匀速圆周运动,所以物块到达A点时速度大小为![]() ,故A错误;
,故A错误;
B.从P到A的过程由动能定理得
![]()
解得
![]()
故B正确;
C.物块进入圆弧后做匀速圆周运动,则物块从A运动到B所用时间

故C正确;
D.物块从A运动到B,由动能定理得
![]()
解得
![]()
故D正确。
故选BCD。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目