题目内容
如图所示，一带电荷量为＋q、质量为m的小物块处于一倾角为37°的光滑斜面上，当整个装置置于一水平向右的匀强电场中，小物块恰好静止．重力加速度取g，sin 37°＝0.6，cos 37°＝0.8.求：
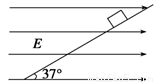
（1）水平向右的电场的电场强度；
（2）若将电场强度减小为原来的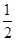
，小物块的加速度是多大；
（3）电场强度变化后小物块下滑距离L时的动能．
【答案】
（1）
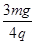； （2）0.3g； （3）0.3mgL
【解析】
试题分析: （1）小物块静止在斜面上，受重力、电场力和斜面支持力，
FNsin37°=qE①
FNcos37°=mg②
由1、②可得电场强度E=；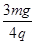
（2）若电场强度减小为原来的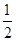
，则变为E'=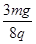
由牛顿第二定律，mgsin37°-q E'cos37°=ma③
可得加速度a=0.3g．
（3）电场强度变化后物块下滑距离L时，重力做正功，电场力做负功，
由动能定理则有：mgLsin37°-qE'Lcos37°=Ek-0④
可得动能Ek=0.3mgL
考点：动能定理的应用；牛顿第二定律；共点力平衡的条件及其应用；电场强度
练习册系列答案
相关题目
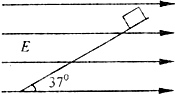如图所示，一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上，当整个装置被置于一水平向右的匀强电场中，小物块恰好静止．重力加速度取g，sin37°=0.6，cos37°=0.8．求：
如图所示，一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上，当整个装置被置于一水平向右的匀强电场中，小物块恰好静止．重力加速度取g，sin 37°=0.6，cos 37°=0.8．
