ЬтФПФкШн
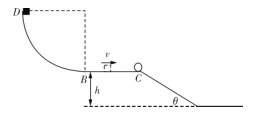
ЁОЬтФПЁПШчЭМЃЌАыОЖ RЃН1.0 m ЕФЫФЗжжЎвЛдВЛЁаЮЙтЛЌЙьЕРЪњжБЗХжУЃЌдВЛЁзюЕЭЕу B гыГЄЮЊ LЃН 0.5 m ЕФЫЎЦНУц BC ЯрЧагк B ЕуЃЌBC РыЕиУцИп hЃН0.45 mЃЌC ЕугывЛЧуНЧЮЊІШЃН37ЁуЕФЙтЛЌаБУцСЌ НгЃЌжЪСП mЃН1.0 kg ЕФаЁЛЌПщДгдВЛЁЩЯФГЕугЩОВжЙЪЭЗХЃЌЕНДядВЛЁ B ЕуЪБаЁЛЌПщЖддВЛЁЕФбЙСІИе КУЕШгкЦфжиСІЕФ 2 БЖЃЌЕБаЁЛЌПщдЫЖЏЕН C ЕуЪБгывЛИіжЪСП MЃН2.0 kg ЕФаЁЧђе§ХіЃЌХіКѓЗЕЛиЧЁКУ ЭЃдк B ЕуЃЌвбжЊЛЌПщгыЫЎЦНУцМфЕФЖЏФІВСвђЪ§ІЬЃН0.1ЁЃ(sin 37ЁуЃН0.6ЃЌcos 37ЁуЃН0.8, g ШЁ 10 m/s2)ЃЌЧѓЃК
(1)аЁЛЌПщгІДгдВЛЁЩЯРы B ЕуЖрИпДІЪЭЗХЃЛ
(2)аЁЛЌПщХізВЧАгыХізВКѓЕФЫйЖШЃЛ
(3)ХізВКѓаЁЧђЕФЕквЛДЮТфЕуОр C ЕуЕФОрРыЁЃ
ЁОД№АИЁП(1) HЃН0.5 m (2) ХіЧАЕФЫйЖШЮЊ![]() ЃЌХіКѓЛЌПщЫйЖШ
ЃЌХіКѓЛЌПщЫйЖШ![]() (3) 0.75m
(3) 0.75m
ЁОНтЮіЁП
(1) ЩшаЁЛЌПщгІДгдВЛЁЩЯРы![]() Еу
Еу![]() ДІЪЭЗХЃЌаЁЛЌПщдЫЖЏЕНBЕуЕФЫйЖШЮЊ
ДІЪЭЗХЃЌаЁЛЌПщдЫЖЏЕНBЕуЕФЫйЖШЮЊ![]() ЃК
ЃК
дкдВЛЁЙьЕРЩЯЛњаЕФмЪиКуЃЌгЩЛњаЕФмЪиКуЖЈТЩгаЃК ![]()
дк![]() ЕужиСІ
ЕужиСІ![]() КЭжЇГжСІ
КЭжЇГжСІ![]() ЕФКЯСІЬсЙЉЯђаФСІЃЌгЩХЃЖйЕкЖўЖЈТЩгаЃК
ЕФКЯСІЬсЙЉЯђаФСІЃЌгЩХЃЖйЕкЖўЖЈТЩгаЃК![]()
гЩЬтвтПЩЕУЃК![]()
СЊСЂЩЯЪННтЕУЃК![]()
(2)ЩшаЁЛЌПщдЫЖЏЕН![]() ЕуЕФЫйЖШЮЊ
ЕуЕФЫйЖШЮЊ![]() ЃЌгЩЖЏФмЖЈРэгаЃК
ЃЌгЩЖЏФмЖЈРэгаЃК![]()
ПЩЕУаЁЛЌПщдк![]() ЕуЕФЫйЖШМДгыаЁЧђХіЧАЕФЫйЖШЃК
ЕуЕФЫйЖШМДгыаЁЧђХіЧАЕФЫйЖШЃК![]()
ХіКѓЛЌПщЗЕЛи![]() ЕуЙ§ГЬЃЌгЩЖЏФмЖЈРэЃК
ЕуЙ§ГЬЃЌгЩЖЏФмЖЈРэЃК![]()
ПЩЕУХіКѓЛЌПщЫйЖШЃК![]()
(3)ЛЌПщКЭаЁЧђХізВЙ§ГЬгЩЖЏСПЪиКуЃК![]() .
.
НтЕУХіКѓаЁЧђЫйЖШЃК![]()
аЁЧђДг![]() ЕузіЦНХздЫЖЏЃЌЩшаЁЧђТфдкЫЎЦНЕиУцЩЯЃЌгЩЦНХздЫЖЏПЩЕУЃК
ЕузіЦНХздЫЖЏЃЌЩшаЁЧђТфдкЫЎЦНЕиУцЩЯЃЌгЩЦНХздЫЖЏПЩЕУЃК
дкЪњжБЗНЯђЃК![]() ЃЌЕФдЫЖЏЪБМф
ЃЌЕФдЫЖЏЪБМф
ЫЎЦНЮЛвЦЮЊ![]()
ТфЕугы![]() ЕуЕФОрРыЮЊ
ЕуЕФОрРыЮЊ![]()
аБУцЕФГЄЮЊ![]() ЃЌЧЁКУЕШгкТфЕугы
ЃЌЧЁКУЕШгкТфЕугы![]() ЕуЕФОрРыЮЊЃЌетЫЕУїаЁЧђЧЁКУТфдкаБУцгыЫЎЦНУцЕФНЛЕуЩЯЁЃ
ЕуЕФОрРыЮЊЃЌетЫЕУїаЁЧђЧЁКУТфдкаБУцгыЫЎЦНУцЕФНЛЕуЩЯЁЃ
злЩЯТфЕугы![]() ЕуЕФОрРыЮЊ
ЕуЕФОрРыЮЊ![]() ЁЃ
ЁЃ