题目内容
质量相同的小球A、B，分别用线悬在等高的O1、O2点，A球的悬线比B球的长，把两球的悬线均拉到水平位置无初速释放，则经最低点时（以悬线的水平方向为零势能点）如图所示．则（ ）分析：A、B两球在运动的过程中，只有重力做功，机械能守恒，比较出初始位置的机械能即可知道在最低点的机械能大小．
根据动能定理mgL=
mv2，可比较出A、B两球的速度大小．根据线速度和角速度的关系比较角速度．
根据动能定理mgL=
| 1 |
| 2 |
解答：解：A、根据动能定理mgL=
mv2，解得：v=
，根据ω=
=
可知，球的角速度小于于B 球的角速度，故A错误；
在最低点，根据牛顿第二定律得：
F-mg=m
得F=mg+m
=3mg，与绳的长度无关．所以两绳拉力大小相等．故B正确．
C、A、B两球在运动的过程中，只有重力做功，机械能守恒，初始位置的机械能相等，所以在最低点，两球的机械能相等．故C错误，D正确．
故选BD．
| 1 |
| 2 |
| gl |
| v |
| l |
|
在最低点，根据牛顿第二定律得：
F-mg=m
| v2 |
| l |
得F=mg+m
| v2 |
| l |
C、A、B两球在运动的过程中，只有重力做功，机械能守恒，初始位置的机械能相等，所以在最低点，两球的机械能相等．故C错误，D正确．
故选BD．
点评：解决本题的关键掌握动能定理和机械能守恒定律，知道摆球在最低点靠合力提供做圆周运动的向心力．
练习册系列答案
相关题目
如图，两个质量相同的小球A、B分别用用线悬在等高的O1、O2点．A球的悬线比B球的长，把两球的悬线拉至水平后无初速释放，则经过最低点时（ ）
两个质量相同的小球a、b用长度不等的细线拴在天花板上的同一点并在空中同一水平面内做匀速圆周运动，如图所示，则a、b两小球具有相同的（ ）
如图所示，一个内壁光滑的圆锥筒的轴线垂直于水平面，圆锥筒固定不动，两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则（ ）| A、球A的线速度必定大于球 B的线速度 | B、球A的角速度必定大于球B的角速度 | C、球A的运动周期必定小于球B的运动周期 | D、球A对筒壁的压力必定大于球B对筒壁的压力 |
如图所示，内壁光滑的圆锥筒的轴线垂直于水平面，圆锥筒固定不动，两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则（ ）| A、球A的线速度一定大于球B的线速度 | B、球A的角速度一定大于球B的角速度 | C、球A对筒壁的压力等于球B对筒壁的压力 | D、球A的运动周期等于球B的运动周期 |
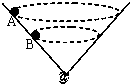如图所示，一个内壁光滑的圆锥筒的轴线垂直于水平面，圆锥筒固定不动，有两个质量相同的小球A和B紧贴着内壁分别在图中所示位置的水平面内作匀速率圆周运动，则以下判断正确的是（ ）| A、球A的线速度大于球B的线速度 | B、球A的向心加速度小于球B的向心加速度 | C、球A对筒壁的压力等于球B对筒壁的压力 | D、球A的运动周期大于球B的运动周期 |