题目内容
如图，重50N的均匀直棒AB，A端靠在光滑墙上，B端拴一轻绳，绳的另一端固定在墙上的C点，棒与竖直方向成45角而处于静止，设棒长为2m，求：（1）AC间的距离；（2）绳上的张力大小．
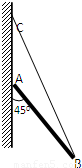
【答案】分析：三个不在同一条直线的力的合力为零时，三个力的作用线必定相交于同一点，对棒受力分析，结合平衡条件和几何关系列式分析即可．
解答：解：（1）对杆受力分析，受到重力、支持力和拉力，如图
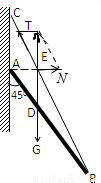
根据三力汇交原理，三个力必定相交与同一点，即图中的E点，的△ABC中，且D是AB的中点．
∴
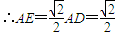
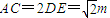
即AC间距为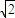
m．
（2）根据几何关系，得到
CE=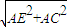
=
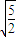
由于力三角形相似于△AEC，故
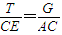
解得
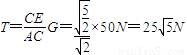
即绳上的张力大小为25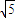
N．
点评：本题关键对杆受力分析，然后根据共点力平衡条件结合三力汇交原理和几何关系列式计算．
解答：解：（1）对杆受力分析，受到重力、支持力和拉力，如图
根据三力汇交原理，三个力必定相交与同一点，即图中的E点，的△ABC中，且D是AB的中点．
∴
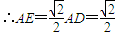
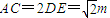
即AC间距为
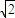m．（2）根据几何关系，得到
CE=
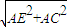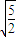
=由于力三角形相似于△AEC，故
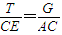
解得
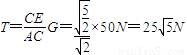
即绳上的张力大小为25
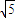N．点评：本题关键对杆受力分析，然后根据共点力平衡条件结合三力汇交原理和几何关系列式计算．
练习册系列答案
名校课堂系列答案
相关题目
如图，重50N的均匀直棒AB，A端靠在光滑墙上，B端拴一轻绳，绳的另一端固定在墙上的C点，棒与竖直方向成450角而处于静止，设棒长为2m，
