题目内容
如图所示，圆柱形容器的内壁上放一个木块，它跟内壁间的动摩擦因数为μ，已知木块中心离转轴的距离为R．当容器以最小转速n=n=
?
| 1 |
| 2π |
|
n=
?
匀速转动时，木块才不至于掉下来．| 1 |
| 2π |
|
分析：当木块恰好不掉下来时，容器的转速n最小，此时木块受到的静摩擦力达到最大．分析木块的受力情况，根据牛顿第二定律，采用正交分解法列方程求解最小的转速n．
解答：解：
当木块恰好不掉下来时，木块受到的静摩擦力达到最大．
根据牛顿第二定律得
f=mg，
N=m?4π2n2R
又f=μN
联立上述三式得
mg=μm4π2n2R
解得
n=
故答案为：n=
当木块恰好不掉下来时，木块受到的静摩擦力达到最大．根据牛顿第二定律得
f=mg，
N=m?4π2n2R
又f=μN
联立上述三式得
mg=μm4π2n2R
解得
n=
| 1 |
| 2π |
|
故答案为：n=
| 1 |
| 2π |
|
点评：本题是圆周运动中临界问题，当两个物体恰好发生相对滑动时，静摩擦力达到最大值是经常用到的临界条件．
练习册系列答案
相关题目
（2007?盐城一模）选修3-3试题：
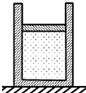如图所示的圆柱形容器内用活塞密封一定质量的理想气体，容器横截面积为S，活塞质量为m，大气压强为p0，重力加速度为g，活塞处于静止状态．现对容器缓缓加热使容器内的气体温度升高t℃，活塞无摩擦地缓慢向上移动了h，在此过程中气体吸收的热量为Q，问：
如图所示的圆柱形容器内用活塞密封一定质量的气体，已知容器横截面积为S，活塞重为G，大气压强为P0．若活塞固定，密封气体温度升高1℃，需吸收的热量为Q1；若活塞不固定而能无摩擦滑动，仍使密封气体温度升高1℃，需吸收的热量为Q2．求在活塞可自由滑动时，密封气体温度升高l℃，活塞上升的高度h．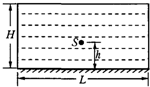
如图所示的圆柱形容器中盛满折射率n=2的某种透明液体，容器底部安装一块平面镜，容器直径L=2H，在圆心正上方高度h处有一点光源S，要使人从液体表面上任意位置处能够观察到点光源S发出的光，h应该满足什么条件？