Question

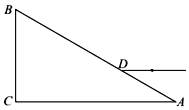
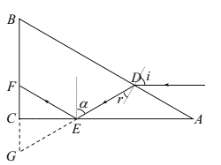
【题目】如图所示，一截面为直角三角形的玻璃棱镜ABC置于真空中，∠A=30°，D点在AB上，AD=L，AB=3L．一条光线平行于AC边从D点射入棱镜，玻璃的折射率为，光在真空中的传播速度为c。

（1）判断AC面是否有光线射出；

（2）求光在棱镜中传播的时间。

Answer 1

【答案】(1)AC边没有光线射出 (2)

【解析】

根据题意画出光路图，由几何知识和折射定律求发生全反射的临界角，根据几何关系求光线在棱镜中传播的距离，由求出光线在棱镜中的传播速度v，再由运动学公式求传播时间t；

解：①入射角为，由折射定律得：

解得折射角：

有几何关系得：

设光线在AC边发生全反射的临界角为，有：

可得，即，因此AC边没有光线射出

②光在棱镜中传播速度为：

BC、DE的延长线交于G点，由几何关系可知，是等边三角形

EF=EG，光在棱镜中传播距离为：

光线在三棱镜传播所用的时间为：

解得：