��Ŀ����
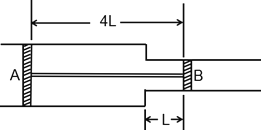
����Ŀ����ͼ��ʾ��ijͬѧ���һ����Ϸװ�ã��õ��������ĵ���ϵͳ��С��ӹܿ�P�������Ҳ�ˮƽ����ΪL����ֱ�߶�ΪH=0.5m���̶�һ��Բ�ιܵ����ܵ�����ƽ����ֱ���뾶R=0.75m���ڱڹ⻬��ͨ����������Q���Ըı䵯��װ�õ�λ�ü���ǣ���������С�����͵�M�����߷������ܵ�������ߵ�N�뿪������عܿ�P������Ϸ�ɹ���С������Ϊ0.2kg���뾶��С�ڹܵ��ھ�������Ϊ�ʵ㣬���ƿ���������gȡ10m/s2����ͬѧij����Ϸȡ�óɹ�������

(1)ˮƽ����L��
(2)С����N���Թܵ�����������
(3)���ɴ���ĵ������ܡ�
���𰸡�(1)![]() (2)
(2) ![]() ��������ֱ���� (3)
��������ֱ���� (3)![]()
��������
(1) P��M��б�����˶�������ߵ��ٶ�ˮƽ�������߽���ܵ����˶�����˼ά����ƽ���˶����㣻M��NΪ����Բ���˶��еĸ�����ģ�ͣ��ö��ܶ���������N��PΪƽ�ף����÷��˶���ʽ��(2)�ˡ���ģ�͵���ߵ㣬�����������ţ�ٵڶ����ɺ�ţ�ٵ���������ѹ����(3)����Ϊ����������������ĵ������ܱ仯�������غ㶨�ɽ�������ȿ��ǵķ���.
(1)��С�����M��ʱ�ٶ�Ϊ![]() ���˶���N���ٶ�Ϊ
���˶���N���ٶ�Ϊ![]() ��
��
��P��M��![]()
![]()
��N��P��![]()
![]()
��M��N���̣��ɹ��ܹ�ϵ�ã�![]()
��ã�![]()
(2)��(1)�ɵã�![]()
![]()
��ã�![]()
��ţ�ٵ������ɿ�֪��С����N���Թܵ���������![]() ��������ֱ����
��������ֱ����
(3)��P��Nȫ���̣��������غ㶨�ɣ�![]()
��ã�![]()

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�