Question

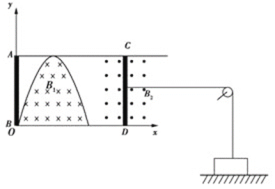
【题目】如图所示，两平行长直金属导轨不计电阻水平放置，间距为L，有两根长度均为L、电阻均为R、质量均为m的导体棒AB、CD平放在金属导轨上。其中棒CD通过绝缘细绳、定滑轮与质量也为m的重物相连，重物放在水平地面上，开始时细绳伸直但无弹力，棒CD与导轨间的动摩擦因数为，最大静摩擦力等于滑动摩擦力，忽略其他摩擦和其他阻力，导轨间有一方向竖直向下的匀强磁场，磁场区域的边界满足曲线方程：，单位为。CD棒处在竖直向上的匀强磁场中。现从时刻开始，使棒AB在外力F的作用下以速度v从与y轴重合处开始沿x轴正方向做匀速直线运动,在运动过程中CD棒始终处于静止状态。

（1）求棒AB在运动过程中，外力F的最大功率；

（2）求棒AB通过磁场区域的过程中，棒CD上产生的焦耳热；

（3）若棒AB在匀强磁场中运动时，重物始终未离开地面,且满足：，求重物所受支持力大小随时间变化的表达式。

Answer 1

【答案】（1）

（2）

（3）①当 0<t≤时，FN=mg

②当<t<时， FN=(1+μ)mg-sin

③当≤t<时， FN=mg

【解析】

（1）当棒AB运动到处时，棒AB的有效切割长度最长，安培力最大，则外力F最大，功率也最大，此时：

F=B1IL=，Pm=Fv

解得：

Pm=；

(2) 棒AB在匀强磁场区域B1的运动过程中，产生的感应电动势为：

E=B1Lvsinx

则感应电动势的有效值为：

E有效=，I有效= t=

可以得到：

Q=Rt=；

(3)当CD棒所受安培力F安=μmg时，设棒AB所在位置横坐标为x0，对棒CD受力分析可得：

=μmg y=Lsinx0

解得：

x0=，x1=L

则：

t1=，t2=

①当 0<t≤时，

则：

FN=mg

②当<t<时，则：

FN=mg+μmg-

即：

FN=(1+μ)mg-sin

③当≤t<时，则：

FN=mg。