��Ŀ����
17�� ijͬѧ���õ��ڲⶨ�����������ٶ�g�����ֵ��ھ�ֹʱ�������������ĵ����·���������Ӧ����ѧ������֪ʶ��Ƴ�һ����������ƫ�����ĵľ����ʵ�飮ʵ�鲽��������
ijͬѧ���õ��ڲⶨ�����������ٶ�g�����ֵ��ھ�ֹʱ�������������ĵ����·���������Ӧ����ѧ������֪ʶ��Ƴ�һ����������ƫ�����ĵľ����ʵ�飮ʵ�鲽��������A�����α꿨�߲��С���ֱ��
B�������ڰ�װ�ú��ÿ̶ȳ߲�����ߵij���L��
C���õ�����С�Ƕ��°ڶ������������������30��ȫ��ʱ�䣬�������T��
D���ı���ߵij��ȣ������6��L��ֵ�Ͷ�Ӧ������T������L1��T1������L12��T2������L3��T3������L4��T4������L5��T5������L6��T6��
��ͬѧ�������õ�ʵ�����ݻ���T2-��L+$\frac{a}{2}$��ͼ����ͼ��ʾ��������ȷ��ͼ��Ӧ��A���A����B����C��������ͼ�пɵó�����ƫ�����ĵľ���h=bcm�������������ٶ�g=$\frac{4{��}^{2}b}{a}$cm/s2��
���� �ɵ������ڹ�ʽ�ɵ�T2-��L+$\frac{a}{2}$����ϵ��ʽ���ɹ�ʽ����ȷ��ͼ��
ͼ����T2��Ľ���Ϊ����ƫ�����ĵľ��룻
���������ٶȱ���ʽ���ͼ��ɵ����ս����
��� �⣺����ƫ�����ĵľ���Ϊh��
�ɵ������ڹ�ʽ�ɵã�
$T=2��\sqrt{\frac{��L+\frac{a}{2}��+h}{g}}$��
��ã�
${T}^{2}=\frac{4{��}^{2}}{g}��L+\frac{a}{2}��+\frac{4{��}^{2}}{g}•h$��
��֪Aͼ����ȷ��
��ͼ�пɵó�����ƫ�����ĵľ���h=b��
�ɵ������ڹ�ʽ��
$T=2��\sqrt{\frac{l}{g}}$��
��ã�
$g=\frac{4{��}^{2}l}{{T}^{2}}$��
��ͼ��ɵã�
$\frac{l}{{T}^{2}}=\frac{b}{a}$��
�ɵ��������ٶ�Ϊ��
$g=\frac{4{��}^{2}b}{a}$��
�ʴ�Ϊ��A��b��$\frac{4{��}^{2}b}{a}$��
���� ����ؼ������յ��ڵ����ڹ�ʽ�������ݹ�ʽ������������ϵ������ȷ��ͼ������ͼ���ж����ͨ�÷�����

��ϰ��ϵ�д�
 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
�����Ŀ
11����UAB=1V����ȷ������ǣ�������
| A�� | ��B��A�ƶ�1C�ĵ�ɣ��糡������-1J | |
| B�� | ��A��B�ƶ�1C�ĵ�ɣ��糡��û������ | |
| C�� | ��B��A�ƶ�1C�ĵ�ɣ��糡������1J | |
| D�� | ��A��B�ƶ�1C�ĵ�ɣ��糡������-1J |
12�� 2013��12��2��1ʱ30�֣����϶����š�̽�����ɳ������������ػ�����������Ƿ������ķ��䣬�״�ʵ����������½������Ѳ�ӿ��죮��̽�����������رգ�������ƽ������������ת�ƹ����ͼ��MN֮���һ�����߱�ʾת�ƹ����һ���֣�P�ǹ���ϵ�һ�㣬ֱ��AB��P���Һ����߹�����У�����˵���в���ȷ���ǣ�������
2013��12��2��1ʱ30�֣����϶����š�̽�����ɳ������������ػ�����������Ƿ������ķ��䣬�״�ʵ����������½������Ѳ�ӿ��죮��̽�����������رգ�������ƽ������������ת�ƹ����ͼ��MN֮���һ�����߱�ʾת�ƹ����һ���֣�P�ǹ���ϵ�һ�㣬ֱ��AB��P���Һ����߹�����У�����˵���в���ȷ���ǣ�������
 2013��12��2��1ʱ30�֣����϶����š�̽�����ɳ������������ػ�����������Ƿ������ķ��䣬�״�ʵ����������½������Ѳ�ӿ��죮��̽�����������رգ�������ƽ������������ת�ƹ����ͼ��MN֮���һ�����߱�ʾת�ƹ����һ���֣�P�ǹ���ϵ�һ�㣬ֱ��AB��P���Һ����߹�����У�����˵���в���ȷ���ǣ�������
2013��12��2��1ʱ30�֣����϶����š�̽�����ɳ������������ػ�����������Ƿ������ķ��䣬�״�ʵ����������½������Ѳ�ӿ��죮��̽�����������رգ�������ƽ������������ת�ƹ����ͼ��MN֮���һ�����߱�ʾת�ƹ����һ���֣�P�ǹ���ϵ�һ�㣬ֱ��AB��P���Һ����߹�����У�����˵���в���ȷ���ǣ�������| A�� | ���Ǿ���P��ʱ�ٶȷ�����P��B | B�� | ���Ǿ���P��ʱ���ٶ�Ϊ0 | ||
| C�� | �����ڴ˶ι���ϣ�����һֱ��С | D�� | ���Ǿ���P��ʱ������С |
9�� ���϶�һ�š�̽�������ص���ת�ƹ��ֱ�������ھ��������200km��P����е�һ�α��������Ƚ�����Բ��������·��У���ͼ��ʾ��֮��������P���־������α�죬����ھ��������200km��Բ�ι������������������Բ���˶����Դˣ�����˵����ȷ���ǣ�������
���϶�һ�š�̽�������ص���ת�ƹ��ֱ�������ھ��������200km��P����е�һ�α��������Ƚ�����Բ��������·��У���ͼ��ʾ��֮��������P���־������α�죬����ھ��������200km��Բ�ι������������������Բ���˶����Դˣ�����˵����ȷ���ǣ�������
 ���϶�һ�š�̽�������ص���ת�ƹ��ֱ�������ھ��������200km��P����е�һ�α��������Ƚ�����Բ��������·��У���ͼ��ʾ��֮��������P���־������α�죬����ھ��������200km��Բ�ι������������������Բ���˶����Դˣ�����˵����ȷ���ǣ�������
���϶�һ�š�̽�������ص���ת�ƹ��ֱ�������ھ��������200km��P����е�һ�α��������Ƚ�����Բ��������·��У���ͼ��ʾ��֮��������P���־������α�죬����ھ��������200km��Բ�ι������������������Բ���˶����Դˣ�����˵����ȷ���ǣ�������| A�� | �����ڹ�������˶����ٶȴ�������ĵ�һ�����ٶ� | |
| B�� | �����ڹ�������˶����ڱ��ڹ�����ϳ� | |
| C�� | �����ڹ�������˶���P��ļ��ٶȴ����ع�����˶���P��ļ��ٶ� | |
| D�� | �����ֹ��������Ƚϣ������ڹ���������еĻ�е����С |
6�� ��ͼ����ʾ�ĵ�·��Mλ�Ե綯�����ڻ���������R�Ĵ�ͷ��һ�˻�����һ�˵Ĺ����У�����ѹ���Ķ���������������ı仯�����ͼ����ʾ����֪��������0.2A����ʱ���綯��û�з���ת�����������Ϊ�������������ж���ȷ���ǣ�������
��ͼ����ʾ�ĵ�·��Mλ�Ե綯�����ڻ���������R�Ĵ�ͷ��һ�˻�����һ�˵Ĺ����У�����ѹ���Ķ���������������ı仯�����ͼ����ʾ����֪��������0.2A����ʱ���綯��û�з���ת�����������Ϊ�������������ж���ȷ���ǣ�������
 ��ͼ����ʾ�ĵ�·��Mλ�Ե綯�����ڻ���������R�Ĵ�ͷ��һ�˻�����һ�˵Ĺ����У�����ѹ���Ķ���������������ı仯�����ͼ����ʾ����֪��������0.2A����ʱ���綯��û�з���ת�����������Ϊ�������������ж���ȷ���ǣ�������
��ͼ����ʾ�ĵ�·��Mλ�Ե綯�����ڻ���������R�Ĵ�ͷ��һ�˻�����һ�˵Ĺ����У�����ѹ���Ķ���������������ı仯�����ͼ����ʾ����֪��������0.2A����ʱ���綯��û�з���ת�����������Ϊ�������������ж���ȷ���ǣ�������| A�� | ����MQΪ��ѹ��V2�Ķ���������������仯��ͼ�� | |
| B�� | ��ԴE������Ϊ2�� | |
| C�� | �綯��������������Ϊ0.9W | |
| D�� | �����������������ֵΪ30�� |
7������ͬ�����ǣ�����˵������ȷ���ǣ�������
| A�� | ͬ�����ǵ��˶����ƽ��һ������ƽ���غ� | |
| B�� | ���е���ͬ�����ǵ����ĵľ��붼��ͬ | |
| C�� | ���е���ͬ�����ǵ���������ͬ | |
| D�� | ͬ���������е����ٶȴ�Сһ��С�ڵ�һ�����ٶ� |
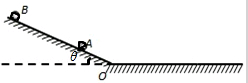 ��ͼ��ʾ��б��⻬����Ǧ�=30�㣬б����ˮƽ��Բ���Խӣ���֪������ȫһ����С����A��B��ֹ��б���ϵij�ʼλ����б���O��ľ���ֱ�ΪLA=L��LB=4L��ˮƽ��ֲ���С����֮��Ķ�Ħ��������Ϊ�̣�����С�����ھ���O����������ʧ���������ٶȴ�СΪg����
��ͼ��ʾ��б��⻬����Ǧ�=30�㣬б����ˮƽ��Բ���Խӣ���֪������ȫһ����С����A��B��ֹ��б���ϵij�ʼλ����б���O��ľ���ֱ�ΪLA=L��LB=4L��ˮƽ��ֲ���С����֮��Ķ�Ħ��������Ϊ�̣�����С�����ھ���O����������ʧ���������ٶȴ�СΪg���� ��ͼ������A��B�ÿ�����ֵ�ϸ����������֪����B������Ϊ80N�������B��֧����Ϊ60N����������B��ϸ����ˮƽ����н�Ϊ30�㣬�������屣�־�ֹ��
��ͼ������A��B�ÿ�����ֵ�ϸ����������֪����B������Ϊ80N�������B��֧����Ϊ60N����������B��ϸ����ˮƽ����н�Ϊ30�㣬�������屣�־�ֹ��