��Ŀ����
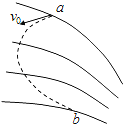
����Ŀ����ͼ��ˮƽ�������ǿ�糡�У���һ�뾶Ϊr�Ĺ⻬��Ե��ֱԲ������糡��������ƽ��ƽ�У�a��bΪ����ڲ�����Բ�ĵȸߵ����㡣һ����Ϊm�������Ϊq(q>0)��С���b���ɾ�ֹ�ͷţ�ǡ�ܵ���������͵㣮��֪�������ٶ�Ϊg��

(1)��糡ǿ�ȵĴ�СE��
(2)����b���С��һ��ֱ���µij��ٶȣ�ʹС�����ع����������Բ���˶�������ٶ�v0���ٶ��
(3)����С���a���ɾ�ֹ�ͷţ���b��ʱС��Թ��ѹ���Ĵ�СNb����С����������ᵯ�𣩣�
���𰸡�(1)![]() (2)
(2)![]() (3)
(3)![]()
��������
(1) ����֪С���b���ɾ�ֹ�ͷţ�ǡ�ܵ���������͵㣬��������ɶ��ܶ����ã�
mgR=qER��![]() .
.
(2)����С���ڸ��ϳ���������ͼ��

��ΪqE=mg����Ч����mg=![]() mg,,��Ч�������ٶ�g=
mg,,��Ч�������ٶ�g=![]() g,
g,![]() =
=![]() ��ҪʹС�����ع����������Բ���˶��������ڵ�Ч��ߵ��ٶ�Ϊv�У�mg=m
��ҪʹС�����ع����������Բ���˶��������ڵ�Ч��ߵ��ٶ�Ϊv�У�mg=m![]()
С���b�㵽��Ч��ߵ��ɶ��ܶ����ã�-qEr(1+![]() )-mgrcos
)-mgrcos![]() =
=![]() m
m![]() -
-![]() m
m![]()
�ɽ�ã�![]()
(3)����С���a���ɾ�ֹ�ͷţ��赽b��ʱ�ٶ�Ϊv��С���a��b�ɶ��ܶ����У�
2qEr=![]() m
m![]()
��b����Nb-qE=m![]()
��ã�Nb=5mg
����ţ�ٵ������ɣ�С��Թ��ѹ���Ĵ�СҲ��5mg������ˮƽ����

��ϰ��ϵ�д�
�����Ŀ