题目内容
1. 如图所示,一辆在水平地面上向右做直线运动的平板车,长度L=6m,质量M=10kg,其上表面水平光滑且距地面高为h=1.25m,A、B是其左右的两端点,在A端固定一个与车绝缘的、质量与大小忽略不计的带电体Q,其电量Q=-5×10-6C.在地面上方的空间存在着沿小车运动方向的、区域足够大的匀强电场(忽略Q的影响),场强大小E=1×107N/C.在t=0时刻,小车速度为v0=7.2m/s,此时将一个质量m=1kg的小球轻放在平板车上距离B端2m处的P点(小球可视为质点,释放时对地的速度为零).经过一段时间,小球脱离平板车并落到地面.已知平板车受到地面的阻力与它对地面的压力成正比,且比例系数μ=0.2,其它阻力不计,重力加速度g=10m/s2.试求:
如图所示,一辆在水平地面上向右做直线运动的平板车,长度L=6m,质量M=10kg,其上表面水平光滑且距地面高为h=1.25m,A、B是其左右的两端点,在A端固定一个与车绝缘的、质量与大小忽略不计的带电体Q,其电量Q=-5×10-6C.在地面上方的空间存在着沿小车运动方向的、区域足够大的匀强电场(忽略Q的影响),场强大小E=1×107N/C.在t=0时刻,小车速度为v0=7.2m/s,此时将一个质量m=1kg的小球轻放在平板车上距离B端2m处的P点(小球可视为质点,释放时对地的速度为零).经过一段时间,小球脱离平板车并落到地面.已知平板车受到地面的阻力与它对地面的压力成正比,且比例系数μ=0.2,其它阻力不计,重力加速度g=10m/s2.试求:(1)从t=0时起,平板车能继续向右运动的最大距离.
(2)小球从t=0时起到离开平板车时所经历的时间.
(3)从t=0时起到小球离开平板车落地时止,带电体Q的电势能的变化量.
分析 (1)从t=0时起,平板车受到向左的电场力,向右做匀减速运动,由牛顿第二定律求得加速度的大小,由运动学速度位移关系公式求出向右运动的最大距离.
(2)根据牛顿第二定律求出小车向右运动的加速度大小,根据运动学公式求出小车向右运动的位移和时间,判断小球是否会从小车的左端掉下,若未掉下,根据牛顿第二定律求出小车向左运动的加速度大小,小球从右端掉下,根据小球小车向左运动的位移求出向左运动的时间,两个时间之和即为小球从轻放到平板车开始至离开平板车所用的时间.
(3)求出小车在小球做自由落体运动时间内的位移,结合小车向右运动的位移和向左运动的位移,求出小车的位移.再求出电场力做功,即可求得带电体Q的电势能的变化量.
解答 解:(1)以平板车为研究对象,根据受力分析和牛顿运动定律有:-μ(m+m)g-EQ=Ma
电场力:F=EQ=1×107N/C×5×10-6C=50N
代入数据解得:a1=-7.2m/s2
x1=$\frac{0-{v}_{0}^{2}}{2{a}_{1}}=\frac{0-7.{2}^{2}}{2×(-7.2)}=3.6$m
(2)因x1<4m,故小球不会从车的左端掉下,小车向右运动的时间t1=$\frac{0-{v}_{0}}{a}=\frac{0-7.2}{-7.2}=1$s
小车向左运动的加速度 a2=$\frac{F-μ(M+m)g}{M}$
代入数据得:a2=2.8m/s2
小球掉下小车时,小车向左运动的距离 x2=x1+$\frac{L}{3}$=5.6m
小车向左运动的时间t2=$\sqrt{\frac{2{x}_{2}}{{a}_{2}}}$=$\sqrt{\frac{2×5.6}{2.8}}$=2s
所以小球从轻放到平板车开始至离开平板车所用的时间 t=t1+t2=1+2=3s
(3)小球刚离开平板车时,小车向左的速度的大小为:v2=a2t2=2.8×2=5.6m/s
小球离开平板车后,车的加速度大小a3=$\frac{F-μMg}{M}$=$\frac{50-0.2×10×10}{10}$=3m/s2
小球离开车子做自由落体的运动 h=$\frac{1}{2}$gt32
代入数据得:t3=0.5s
车子在t3时间内向左运动的距离 x3=v2t3+$\frac{1}{2}$a3t32
代入数据得:t3=3.175m
车子在从t=0时起到小球离开平板车落地时止,向左运动的位移为s
s=x3+x2-x1=3.175+5.6-3.6=5.175m
故在从t=0时起到小球离开平板车落地时止,带电体Q的电势能的变化量为△E,
△E=-Fs=-50×5.175=-258.75J
答:(1)从t=0时起,平板车能继续向右运动的最大距离为3.6m.
(2)小球从t=0时起到离开平板车时所经历的时间为3s.
(3)从t=0时起到小球离开平板车落地时止,带电体Q的电势能的变化量为-258.75J.
点评 本题是一个多过程问题,关键是理清小车在整个过程中的运动情况,结合牛顿第二定律和运动学公式进行求解.

 如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )
如图所示是简式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断正确的是( )| A. | 此时千斤顶对汽车的支持力为2.0×105N | |
| B. | 若继续原方向摇动手把,千斤顶对汽车的支持力将减小 | |
| C. | 若继续原方向摇动手把,两臂受到的压力将增大 | |
| D. | 若继续原方向摇动手把,两臂受到的压力将减小 |
| A. | 该行星质量为M=$\frac{{4{π^2}{R^3}}}{{G{T^2}}}$ | |
| B. | 该行星的同步卫星轨道半径为r=$\root{3}{4}$R | |
| C. | 静置在该行星赤道地面上质量为m的物体对地面的压力为$\frac{{16m{π^2}R}}{T^2}$ | |
| D. | 环绕该行星做匀速圆周运动的卫星线速度必不大于7.9 km/s |
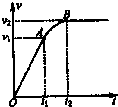 质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
质量为m的汽车在平直的路面上启动,启动过程的速度图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行横轴的直线.已知从t1时刻开始汽车的功率保持不变.整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )| A. | 0-t1时间内,汽车牵引力的数值为m$\frac{v_1}{t_1}$ | |
| B. | t1-t2时间内,汽车的功率等于(m$\frac{{v}_{1}}{{t}_{1}}$+Ff)v2 | |
| C. | tl-t2时间内,汽车的平均速率小于$\frac{{v}_{1}+{v}_{2}}{2}$v2 | |
| D. | 汽车运动的最大速率v2=($\frac{m{v}_{1}}{{F}_{f}{t}_{1}}$+1)v1 |
| A. | 验证牛顿运动定律 | B. | 验证力的平行四边形定则 | ||
| C. | 探究动能定理 | D. | 验证机械能守恒定律 |
| A. | 速度先增大后减小,直到加速度等于零为止 | |
| B. | 速度一直在增大,直到加速度等于零为止 | |
| C. | 位移先增大后减小,直到加速度等于零为止 | |
| D. | 位移一直在增大,直到加速度等于零为止 |
 如图所示,倾角为30°,斜面体固定在地面上,光滑斜面上放一辆小车.一根弹性杆的一端固定在小车上,另一端固定一个重为2N的小球.问:
如图所示,倾角为30°,斜面体固定在地面上,光滑斜面上放一辆小车.一根弹性杆的一端固定在小车上,另一端固定一个重为2N的小球.问: 如图所示,传送带与水平地面间的倾角为θ=37°,从A端到B端长度为s=16m,传送带在电机带动下始终以v=10m/s的速度逆时针运动,在传送带上A端由静止释放一个质量为m=0.5kg的可视为质点的小物体,它与传送带之间的动摩擦因数为μ=0.5,假设最大静摩擦力与滑动摩擦力大小相同,传送带与皮带轮不打滑,g取10m/s2,sin37°=0.6,求:
如图所示,传送带与水平地面间的倾角为θ=37°,从A端到B端长度为s=16m,传送带在电机带动下始终以v=10m/s的速度逆时针运动,在传送带上A端由静止释放一个质量为m=0.5kg的可视为质点的小物体,它与传送带之间的动摩擦因数为μ=0.5,假设最大静摩擦力与滑动摩擦力大小相同,传送带与皮带轮不打滑,g取10m/s2,sin37°=0.6,求: