题目内容
如图所示，为了测定子弹的飞行速度，在一根水平放置的轴杆上固定两个薄圆盘，两圆盘平行间距x=2m，轴杆的转速为60r/s，转动方向如图所示，子弹穿过两圆盘留下的两个弹孔所在的半径间夹角为60°，则该子弹速度可能是（ ）| A、300m/s | B、720m/s | C、1080m/s | D、1440m/s |
分析：通过轴杆的转速，可求出圆盘的角速度，再由两个弹孔所在的半径间的夹角，及圆盘平行间可求出圆盘转动的角度，注意圆的周期性，从而即可求解．
解答：解：子弹的速度是很大的，一般方法很难测出，利用圆周运动的周期性，可以比较方便地测出子弹的速度．子弹从A盘到B盘，盘转过的角度
θ=2πn+
（n=0，1，2…）
盘转动的角速度
ω=
=2πf=2πn=2π?60 rad/s=120π rad/s（n为转速）；
子弹在A、B间运动的时间等于圆盘转动时间，即：
=
所以v=
=
；
v=
（n=0，1，2…）
n=0时，v=720 m/s
n=1时，v=102.8 m/s
n=2时，v=55.4 m/s
…，
最大可能速度为720m/s，故B正确，ACD错误；
故选：B
θ=2πn+
| π |
| 3 |
盘转动的角速度
ω=
| 2π |
| T |
子弹在A、B间运动的时间等于圆盘转动时间，即：
| 2 |
| v |
| θ |
| ω |
所以v=
| 2ω |
| θ |
| 2×120π | ||
2πn+
|
v=
| 720 |
| 6n+1 |
n=0时，v=720 m/s
n=1时，v=102.8 m/s
n=2时，v=55.4 m/s
…，
最大可能速度为720m/s，故B正确，ACD错误；
故选：B
点评：由于圆周运动的周期性，在求解有关运动问题时，要注意其多解性．本题找出在子弹穿过圆盘的时间内，注意圆盘的周期性，圆盘转过的角度是解决本题的关键．
练习册系列答案
相关题目
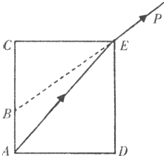如图所示，为了测定水的折射率，某同学将一个高32cm，底面直径24cm的圆筒内注满水，这时从P点恰能看到筒底的A点．把水倒掉后圆筒仍放在原处，这时再从P点观察只能看到B点，B点和C点的距离为18cm．由以上数据计算得水的折射率为多少？若一束光由空气通过圆筒进人水中，则光在水中的传播速度多大（光在真空中速度为3×108m/s）．
圆盘A、B，A、B平行相距2 m，轴杆的转速为360 r/min，在薄圆盘转动不到半周的时间里，子弹穿过两盘留下两个弹孔a、b，测得两孔所在的半径夹
角为30°，则测得该子弹的速度是________.