Question

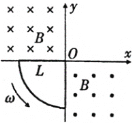
【题目】如图所示，空间中有宽为d的平行边界匀强磁场，磁感应强度大小为B，方向垂直纸面向里，MN、M′N′为磁场边界，MN左侧有一个电荷量为q的带正电粒子P，若P粒子以速度v0垂直MN进入磁场后，离开磁场时的速度方向与M′N′成θ=，不考虑粒子重力，则

A.粒子P进入磁场后做匀速圆周运动，半径为2d

B.粒子P进入磁场时的速度越大，在磁场中运动的时将越长

C.粒子P以速度v0进入磁场后，在磁场运动过程中洛伦兹力的冲量为

D.粒子P进入磁场的速度小于时，粒子P将从MN离开磁场

Answer 1

【答案】D

【解析】

A．粒子运动轨迹如图所示：

由几何关系可得：

解得

故A错误；

B．由洛伦兹力提供向心力得

得

所以速度越大，半径越大，粒子的偏转角越小，由公式

可知，粒子在磁场中的运动时间越小，故B错误；

C．粒子P以速度v0进入磁场后在磁场中的运动时间为

冲量为

故C错误；

D．粒子从MN边射出的临界状态为轨迹与右边界相切，此时半径为d，则有

得

且

即

所以当速度为时，粒子P将从MN离开磁场，故D正确；

故选D。