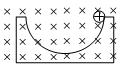
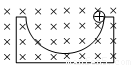
题目内容
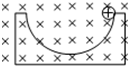 如图,光滑的圆槽固定不动,处于水平向里的匀强磁场中,一带正电小球从斜面右端于圆心等高处由静止沿圆槽下滑,到达最低点.已知小球质量m=0.2g,电量q=1.0×10-6C 圆槽半径 R=1.25m,磁感应强度B=2×102T(g=10m/s2)求:
如图,光滑的圆槽固定不动,处于水平向里的匀强磁场中,一带正电小球从斜面右端于圆心等高处由静止沿圆槽下滑,到达最低点.已知小球质量m=0.2g,电量q=1.0×10-6C 圆槽半径 R=1.25m,磁感应强度B=2×102T(g=10m/s2)求:(1)小球运动到最低点时的速度大小?
(2)小球在第一次到达最低点时圆槽对小球的支持力?
分析:(1)球从最高点到最低点过程,洛伦兹力不做功,只有重力做功,根据动能定理列式求解最低点速度;
(2)球在最低点受重力、洛伦兹力和支持力,合力提供向心力,根据牛顿第二定律列式求解支持力.
(2)球在最低点受重力、洛伦兹力和支持力,合力提供向心力,根据牛顿第二定律列式求解支持力.
解答:解:(1)球从最高点到最低点过程,洛伦兹力不做功,只有重力做功,
根据动能定理,则有:
mv2=mgR
解得:v=
=
=5m/s;
(2)球在最低点受重力、洛伦兹力和支持力,合力提供向心力,
根据牛顿第二定律,结合向心力表达式,则有:
=N-mg;
解得:N=0.2×10-3×
+0.2×10-3×10N=6×10-3 N;
答:(1)小球运动到最低点时的速度大小为5m/s;
(2)小球在第一次到达最低点时圆槽对小球的支持力6×10-3 N.
根据动能定理,则有:
| 1 |
| 2 |
解得:v=
| 2gR |
| 2×10×1.25 |
(2)球在最低点受重力、洛伦兹力和支持力,合力提供向心力,
根据牛顿第二定律,结合向心力表达式,则有:
| mv2 |
| R |
解得:N=0.2×10-3×
| 52 |
| 1.25 |
答:(1)小球运动到最低点时的速度大小为5m/s;
(2)小球在第一次到达最低点时圆槽对小球的支持力6×10-3 N.
点评:本题关键明确物体的运动情况和受力情况,然后根据动能定理和牛顿第二定律列式求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
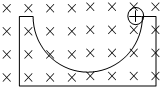 如图,光滑的圆槽固定不动,处于水平向里的匀强磁场中,一带正电小球从与圆心等高处由静止沿圆槽下滑,到达最低点.已知小球质量m=0.1g,电量q=1.0×10-6C 圆槽半径 R=1.25m,磁感应强度B=2×102T(g=10m/s2)
如图,光滑的圆槽固定不动,处于水平向里的匀强磁场中,一带正电小球从与圆心等高处由静止沿圆槽下滑,到达最低点.已知小球质量m=0.1g,电量q=1.0×10-6C 圆槽半径 R=1.25m,磁感应强度B=2×102T(g=10m/s2)