题目内容
 如图,质量m=20kg的物块(可视为质点),以初速度v0=10m/s滑上静止在光滑轨道的质量M=30kg、高h=0.8m的小车的左端,当车向右运动了距离d时(即A处)双方达到共速.现在A处固定一高h=0.8m、宽度不计的障碍物,当车撞到障碍物时被粘住不动,而货物继续在车上滑动,到A处时即做平抛运动,恰好与倾角为53°的光滑斜面相切而沿斜面向下滑动,已知货物与车间的动摩擦因数μ=0.5,(g=10m/s2,sin53°=0.8,cos53°=0.6)求:
如图,质量m=20kg的物块(可视为质点),以初速度v0=10m/s滑上静止在光滑轨道的质量M=30kg、高h=0.8m的小车的左端,当车向右运动了距离d时(即A处)双方达到共速.现在A处固定一高h=0.8m、宽度不计的障碍物,当车撞到障碍物时被粘住不动,而货物继续在车上滑动,到A处时即做平抛运动,恰好与倾角为53°的光滑斜面相切而沿斜面向下滑动,已知货物与车间的动摩擦因数μ=0.5,(g=10m/s2,sin53°=0.8,cos53°=0.6)求:(1)车与货物共同速度的大小v1;
(2)货物平抛时的水平速度v2;
(3)车的长度L与距离d.
分析:(1)由题意,当车向右运动了距离d时(即A处),车与货物双方达到共速.两者组成的系统合外力为零,动量守恒,据此可列式求出共同速度的大小v1;
(2)货物从小车上滑出之后做平抛运动,由平抛运动规律可求出平抛运动的时间和经过斜面顶点时竖直分速度大小,根据速度的分解求解货物平抛时的水平速度v2;
(3)对于货物在车滑行过程,分别对货物和车运用动能定理,列式求解车的长度L与距离d.
(2)货物从小车上滑出之后做平抛运动,由平抛运动规律可求出平抛运动的时间和经过斜面顶点时竖直分速度大小,根据速度的分解求解货物平抛时的水平速度v2;
(3)对于货物在车滑行过程,分别对货物和车运用动能定理,列式求解车的长度L与距离d.
解答: 解:(1)车与货物已经到达共同速度,根据动量守恒定律:
解:(1)车与货物已经到达共同速度,根据动量守恒定律:
mv0=(m+M)v1
得:v1=
=
m/s=4m/s;
(2)货物从小车上滑出之后做平抛运动,由平抛运动规律,得:
h=
gt2
得:t=
=
s=0.4s;
经过斜面顶点时,竖直分速度 vy=gt=10×0.4m/s=4m/s;
在斜面顶点分解速度如图,由
=tan53°,
得:v2=
=
m/s=3m/s;
(3)对于车,由动能定理,得:
μmgd=
M
-0
得:d=
=
m=2.4m
对于货物,全程由动能定理,得:
-μmg(L+d)=
m
-
m
代入数据解得:L=6.7m
答:
(1)车与货物共同速度的大小v1为4m/s.
(2)货物平抛时的水平速度v2为3m/s.
(3)车的长度L与距离d为6.7m.
 解:(1)车与货物已经到达共同速度,根据动量守恒定律:
解:(1)车与货物已经到达共同速度,根据动量守恒定律:mv0=(m+M)v1
得:v1=
| mv0 |
| m+M |
| 20×10 |
| 30+20 |
(2)货物从小车上滑出之后做平抛运动,由平抛运动规律,得:
h=
| 1 |
| 2 |
得:t=
|
|
经过斜面顶点时,竖直分速度 vy=gt=10×0.4m/s=4m/s;
在斜面顶点分解速度如图,由
| vy |
| v2 |
得:v2=
| vy |
| tan53° |
| 4 | ||
|
(3)对于车,由动能定理,得:
μmgd=
| 1 |
| 2 |
| v | 2 1 |
得:d=
| ||||
| μmg |
| ||
| 0.5×20×10 |
对于货物,全程由动能定理,得:
-μmg(L+d)=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 0 |
代入数据解得:L=6.7m
答:
(1)车与货物共同速度的大小v1为4m/s.
(2)货物平抛时的水平速度v2为3m/s.
(3)车的长度L与距离d为6.7m.
点评:本题前两问是多物体多过程的力学问题,把复杂的过程分解成几个分过程是基本思路,然后根据运动学公式和功能关系列式求解.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
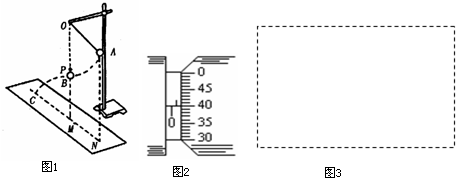
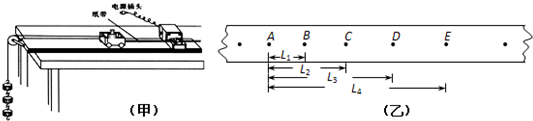
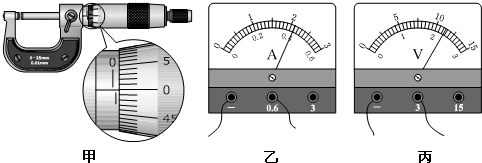
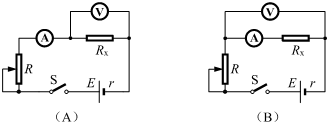
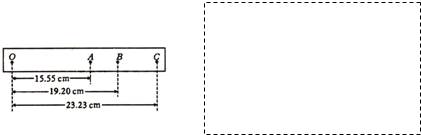
 (1)如图1是用游标卡尺(游标尺上有50个等分刻度)测定某导体的长度、用螺旋测微器测量其厚度时的示数,则长度示数为
(1)如图1是用游标卡尺(游标尺上有50个等分刻度)测定某导体的长度、用螺旋测微器测量其厚度时的示数,则长度示数为
