Question

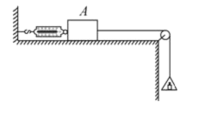
【题目】如图所示,水平杆固定在竖直杆上,两者互相垂直,水平杆上0、A两点连接有两轻绳,两绳的另一端都系在质量为m的小球上,OA=OB=AB,现通过转动竖直杆,使水平杆在水平面内做匀速圆周运动,三角形OAB始终在竖直平面内,若转动过程OA、AB两绳始终处于拉直状态,则下列说法正确的是()

A. OOB绳的拉力范围为

B. OB绳的拉力范围为

C. AB绳的拉力范围为

D. AB绳的拉力范围为

Answer 1

【答案】BC

【解析】

转动的角速度为零时，OB绳的拉力最小，AB绳的拉力最大，当AB绳的拉力刚好为零时，OB绳的拉力最大，根据共点力平衡和牛顿第二定律进行求解。

转动的角速度为零时,OB绳的拉力最小,AB绳的拉力最大,这时二者的值相同,设为，

则，解得

增大转动的角速度,当AB绳的拉力刚好为零时,OB绳的拉力最大,设这时OB绳的拉力为，

,

因此OB绳的拉力范围，AB绳的拉力范围.故BC正确,AD错误.

故选:BC