题目内容
材料:图7(甲)所示是证实玻尔关于原子内部能量量子化的一种实验装置示意图,由电子枪A射出的电子,射入充有氦气的容器B中,电子在O点与氦原子发生碰撞后进入速度选择器C,而氦原子由低能级被激发到高能级.速度选择器C由两个同心的圆弧形电极P1和P2组成,电极间场强方向沿同心圆的半径,当两极间电压为U时,只允许具有确定能量的电子通过,并进入检测装置口,由检测装置口测出电子产生的电流I,改变电压,同时测出I的数值,即可确定碰撞后进入速度选择器的电子能量分布.为了方便研究,作如下假设: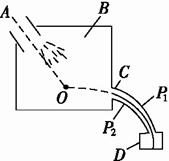
甲 乙
图7
(1)忽略电子的重力;
(2)电子与原子碰撞前,原子静止,原子质量比电子质量大很多,碰撞后原子虽稍微被碰动,但忽略这一能量损失,假定原子未动;
(3)当电子与原子发生弹性碰撞时,电子改变运动方向,但不损失动能;发生非弹性碰撞时,电子损失动能传给原子,使原子内部能量增加.
请根据以上材料和假设回答下列问题:
(1)设速度选择器两极间的电压为U(V)时,允许通过的电子的动能为Ek(eV),写出Ek与U的关系式,设通过选择器的电子轨道半径r=
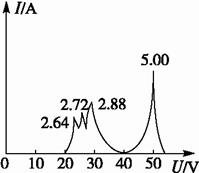
(2)如果电子枪射出电子的动能Ek=50.0 eV,改变P1、P2间电压,测得电流I,得到如图8(乙)所示的I-U图象,图象表明,当电压U为5.00 V、2.88 V、2.72 V、2.64 V时电流出现峰值,试说明在U=5.00 V和U=2.88 V时电子与氦原子碰撞时电子能量的变化.
(3)求氦原子3个激发态的能级En.(设基态的能级E1=0)
(1)Ek=10U ?(2)0 21.2 eV ?(3)E2=21.2 eV E3=22.8 eV E4=23.6 eV?
解析:(1)对于在P1、P2间运动的电子,根据牛顿第二定律得

(2)电子与氦原子碰撞时能量的变化等于电子进入B时的能量50.0 eV减去进入检测装置口D时的能量.即ΔE=50.0 eV-10U eV.由于电压U为5.00 V、2.88 V、2.72 V、2.64 V时电流出现峰值,所以进入检测装置口时电子的能量符合ΔEk=10U eV,所以电压为5.00 V、2.88 V时,电子与氦原子碰撞时电子的能量变化分别为ΔE1=0,ΔE2=(50.0-10×2.28) eV=21.2 eV.
(3)由于电子与原子产生弹性碰撞时,忽略电子的能量损失,而电子与原子发生非弹性碰撞时,电子损失的动能传给原子,使原子能量增大,所以氦原子得到的能量与电子的能量变化相等,故当U为2.88 V、2.72 V、2.64 V时,氦原子在三个激发态的能量分别为:E2=21.2 eV,E3=22.8 eV,E4=23.6 eV.

 阅读快车系列答案
阅读快车系列答案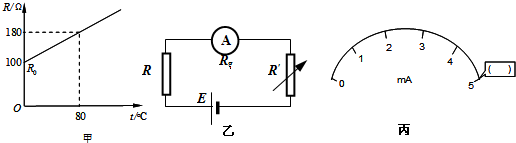


 (1)如图(甲)是由某金属材料制成的电阻R随摄氏温度t变化的图象,若用该电阻与电池(电动势E=1.5V,内阻不计)、电流表(内阻不计)、电阻箱R′串联起来,连接成如图(乙)所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,就得到了一个简单的“金属电阻温度计”.
(1)如图(甲)是由某金属材料制成的电阻R随摄氏温度t变化的图象,若用该电阻与电池(电动势E=1.5V,内阻不计)、电流表(内阻不计)、电阻箱R′串联起来,连接成如图(乙)所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,就得到了一个简单的“金属电阻温度计”.
