题目内容
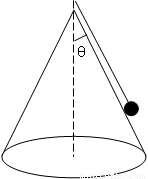
如图所示，在光滑的圆锥体顶端用长为L的细线悬挂一质量为m的小球。圆锥体固定在水平面上不动，其轴线沿竖直方向，母线与轴线之间的夹角θ＝300。现使小球以一定的速率绕圆锥体的轴线在水平面内做圆周运动.
（1）当小球速率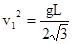
时，求细线对小球的拉力；
（2）当小球速率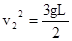
时，求细线对小球的拉力。
【答案】
（1）绳子拉力大小为：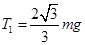
，方向与竖直方向夹角为300且斜向上。
（2）绳子拉力大小为：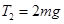
，方向与竖直方向夹角为600且斜向上。
【解析】
试题分析：设速率为v0时，圆锥体对小球的支持力N＝0
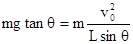
解得：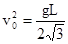
（1）
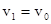，此时N＝0，小球贴着圆锥面做匀速圆周运动。
则绳子拉力大小为：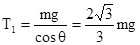
，方向与竖直方向夹角为300且斜向上。
（2）
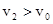，此时小球已经离开圆锥面，设绳子与竖直方向夹角为α，则：
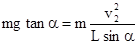
解得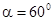
绳子拉力大小为：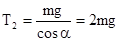
，方向与竖直方向夹角为600且斜向上。
考点：牛顿第二定律；向心力．
点评：本题的关键点在于判断小球是否离开圆锥体表面，不能直接应用向心力公式求解，难度适中．
练习册系列答案
相关题目
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内作半径不同的匀速圆周运动，其中球P的轨道半径较大，则可判定（ ）
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则（ ） 如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则 
| A．球P的角速度较小 | B．球P的向心力较小 |
| C．球P的加速度较大 | D．球P的线速度较大 |
