题目内容
一质量为m=2kg的小滑块，从半径R=1.25m的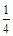
光滑圆弧轨道上的A点由静止滑下，圆弧轨道竖直固定，其末端B切线水平。a、b两轮半径r=0.4m，滑块与传送带间的动摩擦因数µ=0.1，传送带右端点C距水平地面的高度h=1.25m，E为C的竖直投影点。g取10m/s2，求：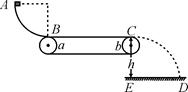
（1）当传送带静止时，滑块恰能在b轮最高点C离开传送带，则BC两点间的距离是多少？
（2）当a、b两轮以某一角速度顺时针转动时，滑块从C点飞出落到地面D点，已知CD两点水平距离为3m。试求：a、b两轮转动的角速度和滑块与传送带间产生的内能。
（1）
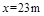（2）Q="1J"
解析试题分析：（1）由题知，滑块从A到B机械能守恒：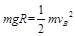
…………………①
滑块由B到C，由动能定理有：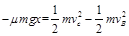
…………………②
滑块恰能在C点离开传送带，有：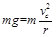
…………………③
联解①②③式得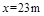： …………………④
（2）设滑块从C点飞出的速度为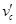
，a、b两轮转动的角速度为ω，则：
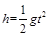…………………⑤
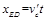…………………⑥
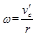…………………⑦
联解⑤⑥⑦式得：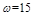
rad/s …………………⑧
滑块在传送带上加速过程，根据牛顿运动定律及功能关系有：
对滑块：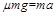
…………………⑨
滑块加速时间：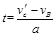
…………………⑩
滑块位移：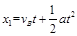
…………………⑾
传送带移动的距离：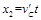
…………………⑿
产生的内能：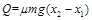
…………………⒀
联解①⑧⑨⑩⑾⑿⒀式得：Q=1J …………………⒁
考点：考查了动能定理以及牛顿第二定律的综合应用
点评：本题的综合性较强，对能力要求较高，难度较大，弄清楚物体的运动过程和受力情况是解题关键．：①物块沿光滑圆弧下滑的过程，机械能守恒；②物块在传送带上做匀减速直线运动．之后做平抛运动
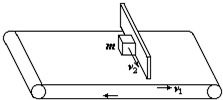一质量为m=2kg的物体置于水平传送带上，随传送带一起以速度v1=2.0m/s向前运动，中途因受到一光滑挡板的阻碍而停止向前运动；现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带，已知板与传送带运动方向垂直（如图所示），物体与传送带间的动摩擦因数为μ=0.3，试求拉力F和挡板对物体的弹力N的大小．
如图所示，水平的传送带以初速度v0=2m/s，加速度
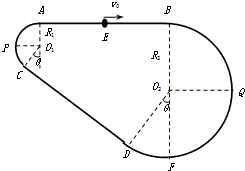如图是放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成：水平直轨AB，半径分别为R1=1.0m和R2=3.0m的弧形轨道，倾斜直轨CD长为L=6m，AB、CD与两圆形轨道相切，其中倾斜直轨CD部分表面粗糙，动摩擦因数为μ=