题目内容
 如图所示,AEBCDO是处于竖直平面内的光滑轨道,AEB是半径为R=1.5m的1/4圆周轨道,CDO是直径为1.5m的半圆轨道.AEB轨道和CDO轨道通过极短的水平轨道(长度忽略不计)平滑连接.半径OA处于水平位置,直径OC处于竖直位置.质量m=0.1kg的小球由A点的正上方高H的P点处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失),小球恰能通过CDO轨道最高点.并落在AEB轨道上的E点,不计空气阻力,g取10m/s2.求:
如图所示,AEBCDO是处于竖直平面内的光滑轨道,AEB是半径为R=1.5m的1/4圆周轨道,CDO是直径为1.5m的半圆轨道.AEB轨道和CDO轨道通过极短的水平轨道(长度忽略不计)平滑连接.半径OA处于水平位置,直径OC处于竖直位置.质量m=0.1kg的小球由A点的正上方高H的P点处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失),小球恰能通过CDO轨道最高点.并落在AEB轨道上的E点,不计空气阻力,g取10m/s2.求:(1)高度H的大小;
(2)当小球通过CDO轨道最低点C时对轨道的压力大小;
(3)θ角的大小.(用反三角函数表示)
分析:(1)小球恰能通过CDO轨道最高点,根据重力等于向心力列式求解O点速度,然后就机械能守恒定律列方程求解;
(2)根据机械能守恒定律求出C点速度,然后根据重力和支持力的合力提供向心力列式求解出支持力,根据牛顿第三定律得到压力;
(3)根据平抛运动的分位移公式列式求解.
(2)根据机械能守恒定律求出C点速度,然后根据重力和支持力的合力提供向心力列式求解出支持力,根据牛顿第三定律得到压力;
(3)根据平抛运动的分位移公式列式求解.
解答:解:(1)因为小球恰能通过O点,故有:mg=m
解得:v0=
小球从P→O机械能守恒,故:mgH=
m
r=
,可得H=
=0.375m
(2)P→C机械能守恒 mg(H+R)=
m
在C点用向心力公式得:NC-mg=m
联立得:N=6mg=6N
(3)小球离开O点做平抛运动,初速度为vO=
由平抛运动规律得:
Rsinθ=vOt
Rcosθ=
gt2
联立得:cos2θ+cosθ-1=0
解得cosθ=
,舍去负值得cosθ=
;
所以θ=arccos
;
答:(1)高度H的大小为0.375m;
(2)当小球通过CDO轨道最低点C时对轨道的压力大小为6N;
(3)θ角的大小为arccos
.
| ||
| r |
解得:v0=
| gr |
小球从P→O机械能守恒,故:mgH=
| 1 |
| 2 |
| v | 2 O |
r=
| R |
| 2 |
| R |
| 4 |
(2)P→C机械能守恒 mg(H+R)=
| 1 |
| 2 |
| v | 2 C |
在C点用向心力公式得:NC-mg=m
| ||
| r |
联立得:N=6mg=6N
(3)小球离开O点做平抛运动,初速度为vO=
| gr |
由平抛运动规律得:
Rsinθ=vOt
Rcosθ=
| 1 |
| 2 |
联立得:cos2θ+cosθ-1=0
解得cosθ=
-1±
| ||
| 2 |
| ||
| 2 |
所以θ=arccos
| ||
| 2 |
答:(1)高度H的大小为0.375m;
(2)当小球通过CDO轨道最低点C时对轨道的压力大小为6N;
(3)θ角的大小为arccos
| ||
| 2 |
点评:本题关键明确小球的运动规律,然后结合机械能守恒定律、向心力公式、牛顿第二定律、平抛运动的规律列式求解.

练习册系列答案
相关题目
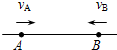 (2008?潍坊模拟)如图所示的直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一带正电粒子以速度vA经过A点向B点运动,经过一段时间后,粒子以速度vB经过B点,且vB与vA方向相反,不计粒子重力,下面说法正确的是( )
(2008?潍坊模拟)如图所示的直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一带正电粒子以速度vA经过A点向B点运动,经过一段时间后,粒子以速度vB经过B点,且vB与vA方向相反,不计粒子重力,下面说法正确的是( ) 如图所示,AB是倾角为θ的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切.一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为μ,重力加速度为g,求:
如图所示,AB是倾角为θ的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切.一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为μ,重力加速度为g,求: 如图所示,0A是一根质量分布不均匀的木棍,它可以绕0点在竖直平面内自由转动,在水平力F的作用下,木棍从悬挂位置缓慢地沿逆时针方向转动,在转到图示虚线位置的过程中( )
如图所示,0A是一根质量分布不均匀的木棍,它可以绕0点在竖直平面内自由转动,在水平力F的作用下,木棍从悬挂位置缓慢地沿逆时针方向转动,在转到图示虚线位置的过程中( ) 2010年2月22日,上海东海大桥风力发电示范工程第 32、33标号的风机在拖轮拖带下由海事局巡逻艇护航,历时t=6h在海上“行走”约 s=54km,安全抵达海上风电场施工吊装现场,如图所示.风电是利用风能使风机的叶片转动,带动发电装置发电的.该风电场共有 34台发电风机,总装机容量(总发电功率)为 P=1.02×105kW,每台风机每年正常工作的时间约为 T=×103 h.试估算以下问题:
2010年2月22日,上海东海大桥风力发电示范工程第 32、33标号的风机在拖轮拖带下由海事局巡逻艇护航,历时t=6h在海上“行走”约 s=54km,安全抵达海上风电场施工吊装现场,如图所示.风电是利用风能使风机的叶片转动,带动发电装置发电的.该风电场共有 34台发电风机,总装机容量(总发电功率)为 P=1.02×105kW,每台风机每年正常工作的时间约为 T=×103 h.试估算以下问题: