题目内容
如图所示，水平转台半径0.2m，可绕通过圆心处的竖直转轴转动．转台的同一半径上放有质量均为0.4kg的小物块A、B（可看成质点），A与转轴间距离0.1m，B位于转台边缘处，A、B间用长O.1m的细线相连，A、B与水平转台间最大静摩擦力均为0.54N，取g=10m/s2（1）当转台的角速度达到多大时细线上出现张力？
（2）当转台的角速度达到多大时A物块开始滑动？
【答案】分析：当转台的角速度比较小时，A、B物块做圆周运动的向心力由静摩擦力提供，随着角速度增大，由Fn=mω2r知向心力增大，由于B物块的转动半径大于A物块的转动半径，B物块的静摩擦力先达到最大静摩擦力，角速度再增大，则细线上出现张力，角速度继续增大，A物块受的静摩擦力也将达最大，这时A物块开始滑动．
解答：解：根据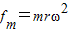
知，ω=
．
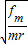知B物体先达到最大静摩擦力，则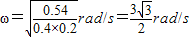
．
（2）当ω继续增大，A受静摩擦力也达到最大静摩擦力时，A开始滑动，设这时的角速度为ω1，
对A物块有：Ffm-FT=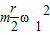
对B物块有：Ffm+FT=mω12r，
联立两式解得：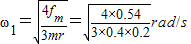
=3rad/s．
答：（1）当转台的角速度达到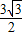
rad/s时，细线上出现张力．
（2）当转台的角速度达到3rad/s时A物块开始滑动．
点评：题的关键是抓住临界状态，隔离物体，正确受力分析，根据牛顿第二定律求解．
解答：解：根据
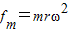知，ω=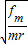．知B物体先达到最大静摩擦力，则
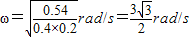．（2）当ω继续增大，A受静摩擦力也达到最大静摩擦力时，A开始滑动，设这时的角速度为ω1，
对A物块有：Ffm-FT=
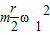
对B物块有：Ffm+FT=mω12r，
联立两式解得：
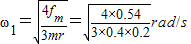=3rad/s．答：（1）当转台的角速度达到
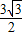rad/s时，细线上出现张力．（2）当转台的角速度达到3rad/s时A物块开始滑动．
点评：题的关键是抓住临界状态，隔离物体，正确受力分析，根据牛顿第二定律求解．
练习册系列答案
相关题目
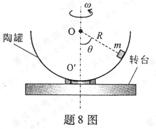
如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合．转台以一定角速度ω匀速转动．一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为60°．重力加速度大小为g．
