Question

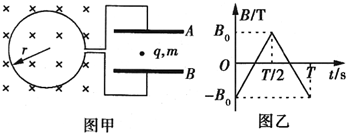
如图甲所示，半径为r、匝数为n的线圈，其两极分别与固定水平放置的平行金属板A、B连接，线圈处在匀强磁场中，磁场方向垂直线圈平面，磁感应强度随时间变化规律如图乙所示．在t=0时刻，将一质量为m、带电荷量为+q、重力不计的粒子从平行金属板中心位置由静止释放，发现在第一个周期内粒子未与金属板相撞．求：

（1）平行金属板间的距离d应满足的条件．
（2）在满足（1）的前提下，在T时间内粒子的最大动能为多大？

Answer 1

【答案】分析：（1）由法拉第电磁感应定律可以求出感应电动势，并由牛顿第二定律与运动学公式相结合，即可求解；
（2）根据题意可知，粒子先做匀加速后做匀减速运动，则速度最大时，动能即为最大，因而即可求解．
解答：解：（1）法拉第电磁感应定律，则有线圈感应电动势E=，
粒子从平行金属板中心位置由静止释放，由发现在第一个周期内粒子未与金属板相撞．
则有
根据牛顿第二定律，则有a=
由以上三式综合，解之得：
（2）根据以上分析，可知，当平行板间距刚好等于d，且当时间为时，粒子的速度达到最大，则动能也最大，
所以根据动能定理，则有W=E_Km-0
而W=qU=q
因此在T时间内粒子的最大动能为．
答：（1）平行金属板间的距离d应满足的条件是：．
（2）在满足（1）的前提下，在T时间内粒子的最大动能为为．
点评：本题是一道综合题，考查了法拉第电磁感应定律与牛顿第二定律，掌握运动学公式的应用，突出匀强磁场场强与电势差的关系的应用，难度较大，分析清楚图象、熟练应用基础知识是正确解题的关键．