题目内容
如图所示,在空间中存在垂直纸面向里的场强为B匀强磁场,其边界AB、CD的宽度为d,在左边界的Q点处有一质量为m,带电量为负q的粒子沿与左边界成30°的方向射入磁场,粒子重力不计.求:(1)带电粒子能从AB边界飞出的最大速度?
(2)若带电粒子能垂直CD边界飞出磁场,穿过小孔进入如图所示的匀强电场中减速至零且不碰到负极板,则极板间电压及整个过程中粒子在磁场中运动的时间?
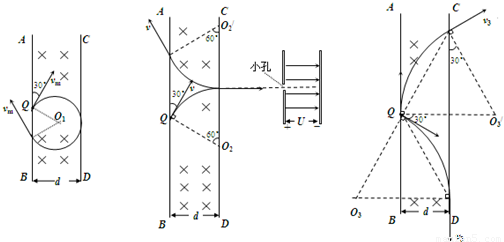
(3)若带电粒子的速度是(2)中的
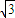 倍,并可以从Q点沿纸面各个方向射入磁场,则粒子能打到CD边界的范围?
倍,并可以从Q点沿纸面各个方向射入磁场,则粒子能打到CD边界的范围?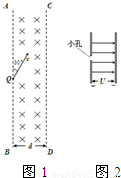
【答案】分析:(1)先作出粒子运动的轨迹,根据几何关系求出粒子能从左边界射出时临界情况的轨道半径,根据洛伦兹力提供向心力公式即可求解最大速度;
(2)根据几何知识求磁场中轨迹半径,由动能定理求极板间电压.
带电粒子能垂直CD边界飞出磁场,穿过小孔进入匀强电场中减速至零,然后由静止返回做匀加速运动,再进入磁场做匀速圆周运动,画出轨迹,确定磁场中运动轨迹对应的圆心角,求出通过磁场的时间.
(3)若带电粒子的速度是(2)中的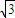 倍,求出轨迹半径,画出轨迹,由几何知识求粒子能打到CD边界的范围.
倍,求出轨迹半径,画出轨迹,由几何知识求粒子能打到CD边界的范围.
解答:解:(1)粒子能从左边界射出,临界情况是轨迹与磁场右边界相切,粒子的运动轨迹如图所示,则有 R+Rcos30°=d
由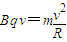 得
得 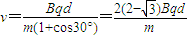
所以粒子能从左边界射出速度应满足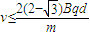 .
.
(2)粒子能从右边界射出,由几何知识得R=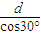
由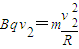 和
和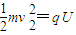
解得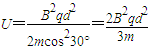
故粒子不碰到右极板所加电压满足的条件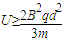
因粒子转过的圆心角为60°,所用时间为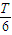 ,而
,而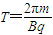
因返回通过磁场所用时间相同,所以总时间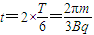
(3)当粒子速度为是(2)中的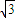 倍时 解得 R′=2d粒子,如图
倍时 解得 R′=2d粒子,如图
由几何关系可得l=2×2dcos30°=2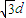
答:
(1)带电粒子能从AB边界飞出的最大速度为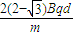 .
.
(2)极板间电压为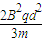 ,整个过程中粒子在磁场中运动的时间为
,整个过程中粒子在磁场中运动的时间为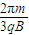 .
.
(3)粒子能打到CD边界的范围为2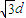 .
.
点评:带电粒子在磁场中的运动要把握其运动规律,在磁场中要注意找出相应的几何关系,从而确定圆心和半径,画出运动轨迹,难度适中.
(2)根据几何知识求磁场中轨迹半径,由动能定理求极板间电压.
带电粒子能垂直CD边界飞出磁场,穿过小孔进入匀强电场中减速至零,然后由静止返回做匀加速运动,再进入磁场做匀速圆周运动,画出轨迹,确定磁场中运动轨迹对应的圆心角,求出通过磁场的时间.
(3)若带电粒子的速度是(2)中的
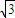 倍,求出轨迹半径,画出轨迹,由几何知识求粒子能打到CD边界的范围.
倍,求出轨迹半径,画出轨迹,由几何知识求粒子能打到CD边界的范围.解答:解:(1)粒子能从左边界射出,临界情况是轨迹与磁场右边界相切,粒子的运动轨迹如图所示,则有 R+Rcos30°=d
由
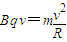 得
得 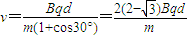
所以粒子能从左边界射出速度应满足
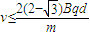 .
.
(2)粒子能从右边界射出,由几何知识得R=
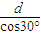
由
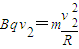 和
和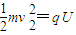
解得
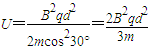
故粒子不碰到右极板所加电压满足的条件
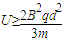
因粒子转过的圆心角为60°,所用时间为
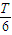 ,而
,而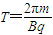
因返回通过磁场所用时间相同,所以总时间
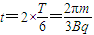
(3)当粒子速度为是(2)中的
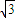 倍时 解得 R′=2d粒子,如图
倍时 解得 R′=2d粒子,如图由几何关系可得l=2×2dcos30°=2
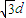
答:
(1)带电粒子能从AB边界飞出的最大速度为
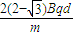 .
.(2)极板间电压为
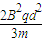 ,整个过程中粒子在磁场中运动的时间为
,整个过程中粒子在磁场中运动的时间为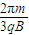 .
.(3)粒子能打到CD边界的范围为2
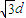 .
.点评:带电粒子在磁场中的运动要把握其运动规律,在磁场中要注意找出相应的几何关系,从而确定圆心和半径,画出运动轨迹,难度适中.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目




